题目内容
16.函数y=cosπx,那么x∈(0,3)内的对称中心个数是3.分析 由题意得,所求的对称中心就是函y=cosπx与x轴交点,可得对称中心为(k+$\frac{1}{2}$,0),k∈z.
解答 解∵余弦函数的对称中心为:(kπ+$\frac{π}{2}$,0)(k∈z),
∴函数y=cosπx,x∈(0,3)的对称中心为:($\frac{1}{2}$,0),($\frac{3}{2}$,0),($\frac{5}{2}$,0).共有3个.
故答案是:3.
点评 本题考查余弦函数的对称中心,体现了转化的数学思想,判断所求的对称中心就是函数 y=cosπx与x轴交点,是解题的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
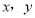 满足约束条件
满足约束条件 ,则
,则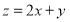 的最大值是( )
的最大值是( ) 是三角形的最大内角,且
是三角形的最大内角,且 ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 如图,为了测定对岸A、B两点之间的距离,在河的一岸定一条基线CD,测得CD=100米,∠ACD=80°,∠BCD=45°,∠BDC=70°,∠ADC=33°,求A、B间的距离.
如图,为了测定对岸A、B两点之间的距离,在河的一岸定一条基线CD,测得CD=100米,∠ACD=80°,∠BCD=45°,∠BDC=70°,∠ADC=33°,求A、B间的距离.