题目内容
1.设函数f(x)=3ax2-2(a+b)x+b(a>0)中,|f(0)|≤2,|f(1)|≤2,(1)证明:0≤x≤1时,有|f(x)|≤2;
(2)是否存在函数f(x)使f($\frac{1}{2}$)=-2?若存在求出函数f(x)的解析式,若不存在,说明理由.
分析 (1)讨论二次函数f(x)在区间[0,1]上的单调性,求出f(x)在[0,1]上的最值,即可证明|f(x)|≤2;
(2)求出a、b的取值范围,再假设存在函数f(x),使f($\frac{1}{2}$)=-2,求出函数f(x)的解析式是否存在即可.
解答 解:(1)证明:∵f(x)=3ax2-2(a+b)x+b=3a(x-$\frac{a+b}{3a}$)2-$\frac{{a}^{2}{+b}^{2}-ab}{3a}$,
∴①当$\frac{a+b}{3a}$≥1或$\frac{a+b}{3a}$≤0时,f(x)在[0,1]上是单调函数,
∴f(1)≤f(x)≤f(0),或f(0)≤f(x)≤f(1),且f(0)+f(1)=a>0;
∴|f(x)|≤max{f(0),f(1)};
②当0<$\frac{a+b}{3a}$<1时,即-a<b<2a,则-$\frac{{a}^{2}{+b}^{2}-ab}{3a}$≤f(x)≤max{f(0),f(1)};
(i)当-a<b≤$\frac{b}{2}$时,则0<a+b≤$\frac{3}{2}$a,
∴f(1)-$\frac{{a}^{2}{+b}^{2}-ab}{3a}$=$\frac{{3a}^{2}{-(a+b)}^{2}}{3a}$≥$\frac{1}{4}$a2>0,
∴|f(x)|≤max{f(0),f(1)};
(ii)当$\frac{a}{2}$<b<2a时,则(b-$\frac{a}{2}$)(b-2a)<0,即a2+b2-$\frac{5}{2}$ab<0,
∴b-$\frac{{a}^{2}{+b}^{2}-ab}{3a}$=$\frac{4ab{-a}^{2}{-b}^{2}}{3a}$>0,即f(0)>$\frac{{a}^{2}{+b}^{2}-ab}{3a}$,
∴|f(x)|≤max{f(0),f(1)};
综上,当0≤x≤1时,|f(x)|≤2;
(2)∵函数f(x)=3ax2-2(a+b)x+b(a>0)中,|f(0)|≤2,|f(1)|≤2;
∴$\left\{\begin{array}{l}{|b|≤2}\\{|a-b|≤2}\\{a>0}\end{array}\right.$,
即$\left\{\begin{array}{l}{-2≤b≤2}\\{-2≤a-b≤2}\\{a>0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{-2≤b≤2}\\{0<a≤4}\end{array}\right.$;
假设存在函数f(x),使f($\frac{1}{2}$)=-2,
∴$\frac{3}{4}$a-(a+b)+b=-2,
解得a=8,不满足0<a≤4;
∴函数f(x)的解析式不存在.
点评 本题考查了求含有字母系数的二次函数在闭区间上的最值问题,也考查了分类讨论思想的应用问题,是综合性题目.

| A. | y=-$\frac{1}{4}$ | B. | y=$\frac{1}{4}$ | C. | x=-$\frac{1}{4}$ | D. | x=$\frac{1}{4}$ |

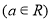 .
.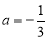 ,求函数
,求函数 在区间
在区间 上的极值;
上的极值; 时,函数
时,函数 只有一个零点,求正数
只有一个零点,求正数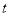 的值.
的值. .
. ,且
,且 对任意
对任意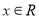 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,且关于
,且关于 的不等式
的不等式 有解,求实数
有解,求实数 的取值范围.
的取值范围. 的展开式的常数项为____________.
的展开式的常数项为____________.