题目内容
设两个不共线的向量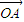 ,
,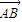 的夹角为θ,且
的夹角为θ,且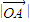 =3,
=3,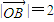 .
.(1)若θ=
 ,求
,求 的值;
的值;(2)若θ为定值,点M在直线OB上移动,
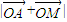 的最小值为
的最小值为 ,求θ的值.
,求θ的值.
【答案】分析:(1)根据两个不共线的向量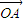 ,
,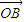 的夹角
的夹角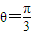 ,及
,及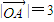 ,
,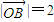 ,结合
,结合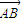 =
=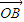 -
-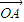 ,我们代入直接求出
,我们代入直接求出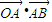 ;
;
(2)由点M在直线OB上,我们设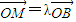 ,结合
,结合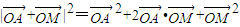 ,分类讨论λ>0(即
,分类讨论λ>0(即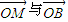 同向)、λ<0(即
同向)、λ<0(即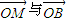 反向)即可求出对应λ的值.
反向)即可求出对应λ的值.
解答:解:(1)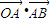 =
=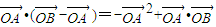
=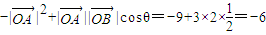 (6分)
(6分)
(2)设 ,
,
则显然λ≠0
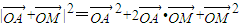
①当λ>0时
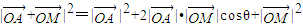
=9+12cosθ•λ+4λ2(*)(8分)
要使得(*)有最小值,
其对称轴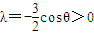 ,
,
即cosθ<0
故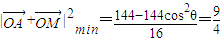 ,
,
解得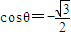 (10分)
(10分)
又0°≤θ≤180°
∴θ=150°(12分)
②当λ<0时
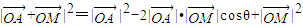
=9+12cosθ•λ+4λ2(#)
要使得(#)有最小值,
其对称轴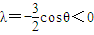 ,
,
即cosθ>0
故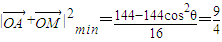 ,
,
解得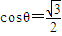
又0°≤θ≤180°
∴θ=30°(15分)
综上所述,θ=30°或150°(16分).
点评:本题考查的知识点是平面向量的数量积运算,向量的模及二次函数的最值问题,考查运算求解能力,考查转化思想.属于基础题.
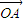 ,
,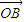 的夹角
的夹角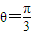 ,及
,及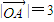 ,
,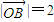 ,结合
,结合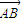 =
=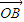 -
-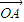 ,我们代入直接求出
,我们代入直接求出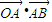 ;
;(2)由点M在直线OB上,我们设
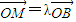 ,结合
,结合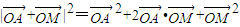 ,分类讨论λ>0(即
,分类讨论λ>0(即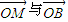 同向)、λ<0(即
同向)、λ<0(即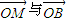 反向)即可求出对应λ的值.
反向)即可求出对应λ的值.解答:解:(1)
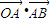 =
=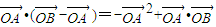
=
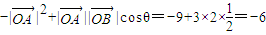 (6分)
(6分)(2)设
 ,
,则显然λ≠0
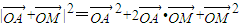
①当λ>0时
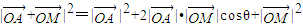
=9+12cosθ•λ+4λ2(*)(8分)
要使得(*)有最小值,
其对称轴
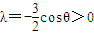 ,
,即cosθ<0
故
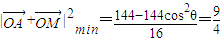 ,
,解得
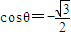 (10分)
(10分)又0°≤θ≤180°
∴θ=150°(12分)
②当λ<0时
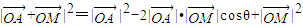
=9+12cosθ•λ+4λ2(#)
要使得(#)有最小值,
其对称轴
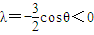 ,
,即cosθ>0
故
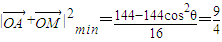 ,
,解得
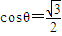
又0°≤θ≤180°
∴θ=30°(15分)
综上所述,θ=30°或150°(16分).
点评:本题考查的知识点是平面向量的数量积运算,向量的模及二次函数的最值问题,考查运算求解能力,考查转化思想.属于基础题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 ,
, 的夹角为θ,且
的夹角为θ,且 =3,
=3,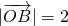 .
. ,求
,求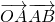 的值;
的值;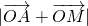 的最小值为
的最小值为 ,求θ的值.
,求θ的值.