题目内容
设两个不共线的向量
,
的夹角为θ,且|
|=3,|
|=2.
(1)若θ=
,求
•
的值;
(2)若θ为定值,点M在直线OB上移动,|
+
|的最小值为
,求θ的值.
| OA |
| AB |
| OA |
| OB |
(1)若θ=
| π |
| 3 |
| OA |
| AB |
(2)若θ为定值,点M在直线OB上移动,|
| OA |
| OM |
| 3 |
| 2 |
分析:(1)根据两个不共线的向量
,
的夹角θ=
,及|
|=3,|
|=2,结合
=
-
,我们代入直接求出
•
;
(2)由点M在直线OB上,我们设
=λ
,结合|
+
|2=
2+2
•
+
2,分类讨论λ>0(即
与
同向)、λ<0(即
与
反向)即可求出对应λ的值.
| OA |
| OB |
| π |
| 3 |
| OA |
| OB |
| AB |
| OB |
| OA |
| OA |
| AB |
(2)由点M在直线OB上,我们设
| OM |
| OB |
| OA |
| OM |
| OA |
| OA |
| OM |
| OM |
| OM |
| OB |
| OM |
| OB |
解答:解:(1)
•
=
•(
-
)=-
2+
•
=-|
|2+|
||
|cosθ=-9+3×2×
=-6(6分)
(2)设
=λ
,
则显然λ≠0
|
+
|2=
2+2
•
+
2
①当λ>0时
|
+
|2=|
|2+2|
|•|
|cosθ+|
|2
=9+12cosθ•λ+4λ2(*)(8分)
要使得(*)有最小值,
其对称轴λ=-
cosθ>0,
即cosθ<0
故|
+
|2min=
=
,
解得cosθ=-
(10分)
又0°≤θ≤180°
∴θ=150°(12分)
②当λ<0时
|
+
|2=|
|2-2|
|•|
|cosθ+|
|2
=9+12cosθ•λ+4λ2(#)
要使得(#)有最小值,
其对称轴λ=-
cosθ<0,
即cosθ>0
故|
+
|2min=
=
,
解得cosθ=
又0°≤θ≤180°
∴θ=30°(15分)
综上所述,θ=30°或150°(16分).
| OA |
| AB |
| OA |
| OB |
| OA |
| OA |
| OA |
| OB |
=-|
| OA |
| OA |
| OB |
| 1 |
| 2 |
(2)设
| OM |
| OB |
则显然λ≠0
|
| OA |
| OM |
| OA |
| OA |
| OM |
| OM |
①当λ>0时
|
| OA |
| OM |
| OA |
| OA |
| OM |
| OM |
=9+12cosθ•λ+4λ2(*)(8分)
要使得(*)有最小值,
其对称轴λ=-
| 3 |
| 2 |
即cosθ<0
故|
| OA |
| OM |
| 144-144cos2θ |
| 16 |
| 9 |
| 4 |
解得cosθ=-
| ||
| 2 |
又0°≤θ≤180°
∴θ=150°(12分)
②当λ<0时
|
| OA |
| OM |
| OA |
| OA |
| OM |
| OM |
=9+12cosθ•λ+4λ2(#)
要使得(#)有最小值,
其对称轴λ=-
| 3 |
| 2 |
即cosθ>0
故|
| OA |
| OM |
| 144-144cos2θ |
| 16 |
| 9 |
| 4 |
解得cosθ=
| ||
| 2 |
又0°≤θ≤180°
∴θ=30°(15分)
综上所述,θ=30°或150°(16分).
点评:本题考查的知识点是平面向量的数量积运算,向量的模及二次函数的最值问题,考查运算求解能力,考查转化思想.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•卢湾区一模)已知
(2012•卢湾区一模)已知
 已知
已知 、
、 是两个不共线的非零向量.
是两个不共线的非零向量. ,
,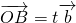 (t∈R),
(t∈R),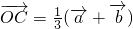 ,当A、B、C三点共线时,求t的值.
,当A、B、C三点共线时,求t的值.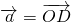 ,
,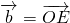 ,
, 上一动点,设
上一动点,设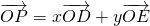 (x,y∈R),求x+y的最大值.
(x,y∈R),求x+y的最大值.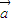 、
、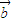 是两个不共线的非零向量.
是两个不共线的非零向量.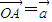 ,
, (t∈R),
(t∈R), ,当A、B、C三点共线时,求t的值.
,当A、B、C三点共线时,求t的值.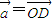 ,
,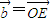 ,
,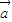 与
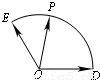
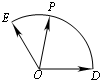
与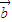 夹角为120°,|
夹角为120°,|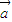 |=|
|=|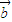 |=1,点P是以O为圆心的圆弧
|=1,点P是以O为圆心的圆弧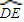 上一动点,设
上一动点,设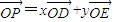 (x,y∈R),求x+y的最大值.
(x,y∈R),求x+y的最大值.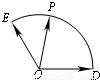
 、
、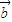 是两个不共线的非零向量.
是两个不共线的非零向量.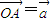 ,
,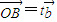 (t∈R),
(t∈R),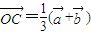 ,当A、B、C三点共线时,求t的值.
,当A、B、C三点共线时,求t的值.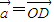 ,
,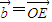 ,
,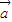 与
与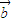 夹角为120°,|
夹角为120°,|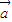 |=|
|=|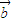 |=1,点P是以O为圆心的圆弧
|=1,点P是以O为圆心的圆弧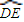 上一动点,设
上一动点,设 (x,y∈R),求x+y的最大值.
(x,y∈R),求x+y的最大值.