题目内容
7.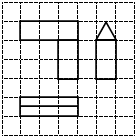 如图,网格纸的小正方形的边长是1,粗线画出的是一个几何体的三视图,则这个几何体的体积为( )
如图,网格纸的小正方形的边长是1,粗线画出的是一个几何体的三视图,则这个几何体的体积为( )| A. | $\frac{5}{2}$ | B. | $\frac{7}{2}$ | C. | 2+$\frac{\sqrt{3}}{4}$ | D. | 3+$\frac{\sqrt{3}}{3}$ |
分析 根据几何体的三视图,得出该几何体是三棱柱与长方体的组合体,结合图中数据即可求出它的体积.
解答 解:根据几何体的三视图,得;
该几何体是上部为三棱柱,下部为长方体的组合体,
且三棱柱的底面为底面边长是1,底边上的高是1,三棱柱的高是3,
长方体的底面是边长为1的正方形,高是2;
所以该几何体的体积为
V=V三棱柱+V长方体=$\frac{1}{2}$×1×1×3+1×1×2=$\frac{7}{2}$.
故选:B.
点评 本题考查了空间几何体三视图的应用问题,解题的关键是根据三视图得出几何体的结构特征,是基础题目.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
15.函数y=cos(πx+2)的最小正周期是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
2.已知集合A={x|x2-2x-3≤0},B={x|log2(x2-x)>1}则A∩B=( )
| A. | (2,3) | B. | (2,3] | C. | (-3,-2) | D. | [-3,-2) |
6.已知f(x)在x0处可导,则$\underset{lim}{h→0}\frac{f({x}_{0}+h)-f({x}_{0})}{2h}$等于( )
| A. | $\frac{1}{2}f′({x}_{0})$ | B. | f′(x0) | C. | 2f′(x0) | D. | 4f′(x0) |