题目内容
12.函数y=sin3x+cos3x的值域为[-$\sqrt{2}$,$\sqrt{2}$],最小正周期为$\frac{2π}{3}$.分析 利用三角函数的恒等变换,化简函数y,求出函数y的值域和最小正周期.
解答 解:∵函数y=sin3x+cos3x
=$\sqrt{2}$($\frac{\sqrt{2}}{2}$sin3x+$\frac{\sqrt{2}}{2}$cos3x)
=$\sqrt{2}$sin(3x+$\frac{π}{4}$),
且-1≤sin(3x+$\frac{π}{4}$)≤1,
∴-$\sqrt{2}$≤$\sqrt{2}$sin(3x+$\frac{π}{4}$)≤$\sqrt{2}$,
即函数y的值域为[-$\sqrt{2}$,$\sqrt{2}$];
其最小正周期为T=$\frac{2π}{3}$.
故答案为:[-$\sqrt{2}$,$\sqrt{2}$],$\frac{2π}{3}$.
点评 本题考查了三角函数的化简与求值的应用问题,也考查了三角函数的恒等变换问题,是基本知识的考查.

练习册系列答案
相关题目
2.假如某天我校某班有3男2女五位同学均获某年北大、清华、复旦三大名校的保送资格,那么恰有2男1女三位同学保送北大的概率是( )
| A. | $\frac{6}{125}$ | B. | $\frac{2}{81}$ | C. | $\frac{24}{125}$ | D. | $\frac{8}{81}$ |
3.一只袋内装有m个白球,n-m个黑球,连续不放回地从袋中取球,直到取出黑球为止,设此时取了ξ个白球,下列概率等于$\frac{(n-m{)A}_{m}^{2}}{{A}_{n}^{3}}$的是( )
| A. | P(ξ=3) | B. | P(ξ≥2) | C. | P(ξ≤3) | D. | P(ξ=2) |
7. 如图,网格纸的小正方形的边长是1,粗线画出的是一个几何体的三视图,则这个几何体的体积为( )
如图,网格纸的小正方形的边长是1,粗线画出的是一个几何体的三视图,则这个几何体的体积为( )
 如图,网格纸的小正方形的边长是1,粗线画出的是一个几何体的三视图,则这个几何体的体积为( )
如图,网格纸的小正方形的边长是1,粗线画出的是一个几何体的三视图,则这个几何体的体积为( )| A. | $\frac{5}{2}$ | B. | $\frac{7}{2}$ | C. | 2+$\frac{\sqrt{3}}{4}$ | D. | 3+$\frac{\sqrt{3}}{3}$ |
4.如图是成品加工流程图,从图中可以看出,即使是一件不合格产品,也必须经过多少道工序( )
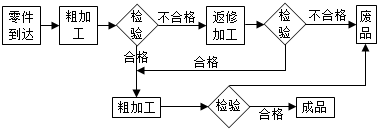

| A. | 6 | B. | 5或7 | C. | 5 | D. | 5或6或7 |
8.函数y=$\frac{8}{x-1}$+1的单调递减区间是( )
| A. | (-∞,1)∪(1,+∞) | B. | (-∞,-1)∪(-1,+∞) | C. | (-∞,1),(1,+∞) | D. | (-∞,-1),(-1,+∞) |
9.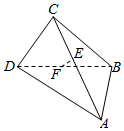 已知在四面体ABCD中,E、F分别是AC、BD的中点,若CD=2,AB=4,EF⊥CD,则EF与AB所成的角为( )
已知在四面体ABCD中,E、F分别是AC、BD的中点,若CD=2,AB=4,EF⊥CD,则EF与AB所成的角为( )
 已知在四面体ABCD中,E、F分别是AC、BD的中点,若CD=2,AB=4,EF⊥CD,则EF与AB所成的角为( )
已知在四面体ABCD中,E、F分别是AC、BD的中点,若CD=2,AB=4,EF⊥CD,则EF与AB所成的角为( )| A. | 90° | B. | 45° | C. | 60° | D. | 30° |