题目内容
18.经过原点的直线l与圆x2+y2-6x-4y+9=0相交于两个不同点A,B,求线段AB的中点M的轨迹方程.分析 法一、适当引入参数,设出中点坐标,通过联立方程组,利用韦达定理,再消去参数得所求轨迹;
法二、设出A(x1,y1),B(x2,y2),代入圆的方程,作差,利用中点公式,结合直线的斜率,消去参数求中点轨迹方程.
解答 解:法一、由题意可知直线l的斜率存在,设直线方程为y=kx,
联立$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}-6x-4y+9=0}\\{y=kx}\end{array}\right.$,消去y得,(1+k2)x2-(6+4k)x+9=0.
设此方程的两根为x1、x2,AB的中点坐标为M(x,y),
则由韦达定理和中点坐标公式,得x=$\frac{{x}_{1}+{x}_{2}}{2}=\frac{6+4k}{2(1+{k}^{2})}$=$\frac{3+2k}{1+{k}^{2}}$.①
又点M在直线y=kx上,
∴y=kx.
∴k=$\frac{y}{x}$.②
将②代入①,得x=$\frac{3+2•\frac{y}{x}}{1+(\frac{y}{x})^{2}}$(x≠0),整理得x2+y2-3x-2y=0.
故轨迹是圆x2+y2-3x-2y=0位于已知圆内的部分;
解法二、设A(x1,y1),B(x2,y2),则:
x12+y12-6x1-4y1+9=0,①
x22+y22-6x2-4y2+9=0,②
①-②,得(x12-x22)+(y12-y22)-6(x1-x2)-4(y1-y2)=0.
设AB的中点为(x,y),则x1+x2=2x,y1+y2=2y.
代入上式,有2x(x1-x2)+2y(y1-y2)-6(x1-x2)-4(y1-y2)=0,
即(2x-6)(x1-x2)+(2y-4)(y1-y2)=0.
∴$\frac{x-3}{y-2}=-\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-k.③
又∵y=kx,④
由③④得x2+y2-3x-2y=0.
故所求轨迹为已知圆内的一段弧.
点评 本题考查与圆有关的轨迹问题.法一为参数法,适当引入参数,再消去参数得所求轨迹;法二为“点差法”,是求中点轨迹的一种常用方法,该题是中档题.

| A. | 5050 | B. | 4950 | C. | 197 | D. | 195 |
| A. | P(ξ=3) | B. | P(ξ≥2) | C. | P(ξ≤3) | D. | P(ξ=2) |
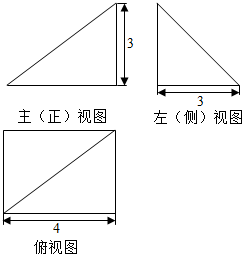
| A. | 12 | B. | 18 | C. | 24 | D. | 36 |
 如图,网格纸的小正方形的边长是1,粗线画出的是一个几何体的三视图,则这个几何体的体积为( )
如图,网格纸的小正方形的边长是1,粗线画出的是一个几何体的三视图,则这个几何体的体积为( )| A. | $\frac{5}{2}$ | B. | $\frac{7}{2}$ | C. | 2+$\frac{\sqrt{3}}{4}$ | D. | 3+$\frac{\sqrt{3}}{3}$ |