题目内容
在△ABC中，D为BC中点，∠BAD=45°，∠CAD=30°，AB=
，则AD= ．
| 2 |
分析：根据中点想到将三角形补成平行四边形，三角形ABE中已知两个角和一个边利用正弦定义求出另一边即可．
解答：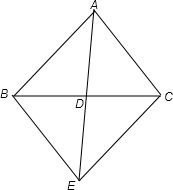
解：先将△ABC补成平行四边形
则∠AEB=30°，∠ABE=105°，
利用正弦定理得
=
，
解得AD=
，
故答案为
解：先将△ABC补成平行四边形则∠AEB=30°，∠ABE=105°，
利用正弦定理得
| ||
| sin30° |
| 2AD |
| sin105° |
解得AD=
| ||
| 2 |
故答案为
| ||
| 2 |
点评：本题考查了正弦定理的应用，正弦定理沟通了三角函数与三角形有关性质，反映了事物之间的内在联系及一定条件下的相互转化．，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
在△ABC中，D为BC的中点，已知
=
，
=
，则下列向量一定与
同向的是（ ）
| AB |
| a |
| AC |
| b |
| AD |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
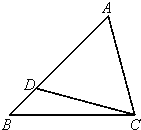如图，在△ABC中，D为边AB上一点，DA=DC．已知B=