Question

【题目】某厂生产某种产品的年固定成本为250万元，每生产x千件，需另投入成本为C（x）万元，当年产量不足80千件时，C（x）＝x2＋10x（万元）；当年产量不少于80千件时，C（x）＝51x＋－1 450（万元）．通过市场分析，若每件售价为500元时，该厂年内生产的商品能全部销售完．

（1）写出年利润L（万元）关于年产量x（千件）的函数解析式；

（2）年产量为多少千件时，该厂在这一商品的生产中所获利润最大？

Answer 1

【答案】（1）；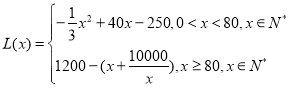

（2）年产量为100千克时，该厂在这一商品生产中所获利润最大．

【解析】

试题分析：（1）本题是函数应用题，解题时需掌握日常生活中的关系式：利润＝收入－成本，收入＝销售量×单价，由此可得利润函数，本题中要注意由于成本与的取值范围有关，因此要分类，其次要注意单位要统；（2）求利润最大值，对分段函数可分类求最大值，然后再找两者中较大的一个．其中一段手二次函数的性质求最大值，一个用基本不等式求最大值．

试题解析：时，

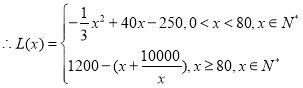
综上所述，当x=100时，L（X）取得最大值1000，即年产量为100千克时，该厂在这一商品生产中所获利润最大。