Question

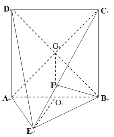
【题目】如图，直二面角D—AB—E中，四边形ABCD是边长为2的正方形，AE=EB，F为CE上的点，且BF⊥平面ACE.

（1）求证：AE⊥平面BCE；

（2）求二面角B—AC—E的余弦值.

Answer 1

【答案】（1）详见解析（2）

【解析】

试题分析：（1）欲证AE⊥平面BCE，由题设条件知可先证BF⊥AE，CB⊥AE，再由线面垂直的判定定理得出线面垂直即可；（2）求二面角B-AC-E的正弦值，需要先作角，连接BD交AC交于G，连接FG，可证得∠BGF是二面B-AC-E的平面角，在△BFG中求解即可

试题解析：（1）证明：∵平面ACE. ------------------1分

∵二面角D—AB—E为直二面角，且，

，

平面ABE ------------------3分

------------------4分

又∵BF∩CB=B，

------------------5分

（2）解：连结BD交AC于G，连结FG.

∵平面ACE，∴AC

又∵正方形ABCD中，，且BF∩BG=B

∴

即为二面角B—AC—E的平面角------------------8分

∵，，，

在中，可求，

∴在中，FG=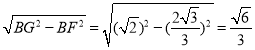

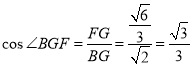∴，即二面角B—AC—E的余弦值为 ------------12分