题目内容
【题目】选修4—4:坐标系与参数方程。
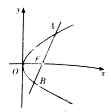
在平面直角坐标系xOy中,已知曲线![]()
![]() ,以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
,以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() .
.
(1)将曲线![]() 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的![]() 、2倍后得到曲线
、2倍后得到曲线![]() ,试写出直线
,试写出直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的参数方程;
的参数方程;
(2)在曲线![]() 上求一点P,使点P到直线
上求一点P,使点P到直线![]() 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
【答案】(1)直线![]() :
:![]() ,曲线
,曲线![]() :
: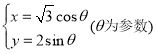 ;(2)点P(
;(2)点P(![]() ),此时
),此时![]() .
.
【解析】
试题分析:(1)由公式![]() 可化直线的极坐标方程为直角坐标方程,设曲线
可化直线的极坐标方程为直角坐标方程,设曲线![]() 点坐标为
点坐标为![]() 与之对应的曲线
与之对应的曲线![]() 上的点为
上的点为![]() ,则
,则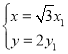 ,解得
,解得![]() 代入曲线
代入曲线![]() 的方程可得
的方程可得![]() 方程;(2)由
方程;(2)由![]() 参数方程要设设点P的坐标
参数方程要设设点P的坐标![]() ,由点P到直线
,由点P到直线![]() 的距离公式求得距离
的距离公式求得距离![]() ,由两角和与差的正弦公式及正弦函数的性质可得最大值.
,由两角和与差的正弦公式及正弦函数的性质可得最大值.
试题解析:(1) 由题意知,直线![]() 的直角坐标方程为:
的直角坐标方程为:![]() ,
,
∵曲线![]() 的直角坐标方程为:
的直角坐标方程为:![]() ,
,
∴曲线![]() 的参数方程为:
的参数方程为: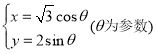 .
.
(2)设点P的坐标![]() ,则点P到直线
,则点P到直线![]() 的距离为:
的距离为:
![]() ,
,
∴当sin(600-θ)=-1时,点P(![]() ),此时
),此时![]() .
.

练习册系列答案
相关题目
【题目】某车间将10名技工平均分为甲、乙两组加工某种零件,在单位时间内每名技工加工零件若干,其中合格零件的个数如下表:
1号 | 2号 | 3号 | 4号 | 5号 | |
甲组 | 4 | 5 | 7 | 9 | 10 |
乙组 | 5 | 6 | 7 | 8 | 9 |
(1)分别求出甲、乙两组技工在单位时间内完成合格零件的平均数及方差,并由此分析两组技工的技术水平;
(2)质检部门从该车间甲、乙两组中各随机抽取一名技工,对其加工的零件进行检测,若两人完成合格零件个数之和超过12件,则称该车间“质量合格”,求该车间“质量合格”的概率.