题目内容
、设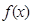 是定义在
是定义在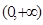 上的增函数,对任意
上的增函数,对任意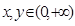 ,满足
,满足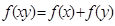 。
。
(1)、求证:①当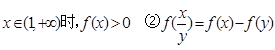
(2)、若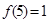 ,解不等式
,解不等式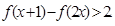
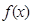 是定义在
是定义在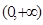 上的增函数,对任意
上的增函数,对任意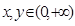 ,满足
,满足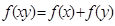 。
。(1)、求证:①当
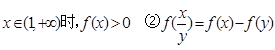
(2)、若
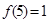 ,解不等式
,解不等式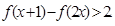
(1) 见解析; (2) 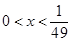 。
。
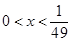 。
。本试题主要是考查了抽象函数的赋值思想的运用以及不等式的求解的综合问题。
(1)
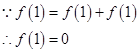
又 在(0 ,+∞)上是增函数,所以
在(0 ,+∞)上是增函数,所以 >0并且
>0并且
由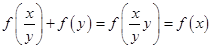 得
得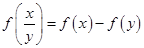
(2)因为
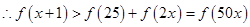 ,利用
,利用 在(0 ,+∞)上是增函数解得不等式。
在(0 ,+∞)上是增函数解得不等式。
(1) ①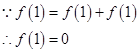 又
又 在(0 ,+∞)上是增函数,所以
在(0 ,+∞)上是增函数,所以 >0
>0
②由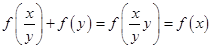 得
得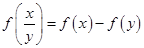 -----7分
-----7分
(2) ∵
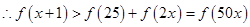 且
且 在(0 ,+∞)上是增函数
在(0 ,+∞)上是增函数
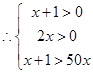 解得
解得 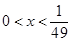 -------------14分
-------------14分
(1)
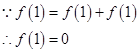
又
 在(0 ,+∞)上是增函数,所以
在(0 ,+∞)上是增函数,所以 >0并且
>0并且由
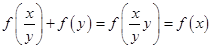 得
得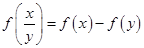
(2)因为

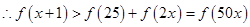 ,利用
,利用 在(0 ,+∞)上是增函数解得不等式。
在(0 ,+∞)上是增函数解得不等式。(1) ①
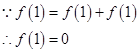 又
又 在(0 ,+∞)上是增函数,所以
在(0 ,+∞)上是增函数,所以 >0
>0②由
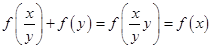 得
得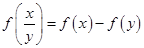 -----7分
-----7分(2) ∵

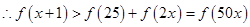 且
且 在(0 ,+∞)上是增函数
在(0 ,+∞)上是增函数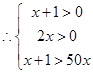 解得
解得 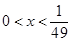 -------------14分
-------------14分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
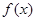 在区间[0,a](a>0)上是单调函数,且f(0)·f(a)<0,则函数
在区间[0,a](a>0)上是单调函数,且f(0)·f(a)<0,则函数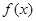 是定义在R上的奇函数,且
是定义在R上的奇函数,且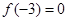 。当
。当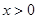 时,有
时,有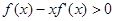 成立,则不等式
成立,则不等式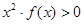 的解集是
的解集是

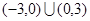
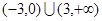
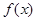 =
=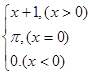 求
求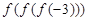 的值。
的值。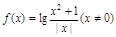 ,有下列命题:
,有下列命题: 轴对称; ②当
轴对称; ②当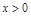 时,
时,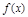 是增函数;当
是增函数;当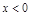 时,
时,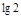 ; ④当
; ④当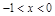 和
和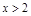 时,
时, )=f(x)-f(y).
)=f(x)-f(y). )<2.
)<2.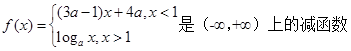 ,那么
,那么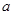 的取值范围( )
的取值范围( ) 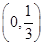 C.
C.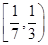 D.
D.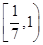
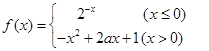
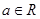 ,则下列结论正确的是( )
,则下列结论正确的是( )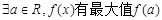
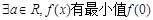
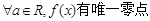
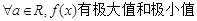
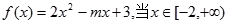 时是增函数,则m的取值范围是( )
时是增函数,则m的取值范围是( )