题目内容
(22)已知{an}是由非负整数组成的数列,满足
a1=0,a2=3,an+1an=(an-1+2)(an-2+2),n=3,4,5,….
(Ⅰ)求a3;
(Ⅱ)证明an=an-2+2,n=3,4,5,…;
(Ⅲ)求{an}的通项公式及其前n项和Sn.
(22)本小题主要考查数列与等差数列前n项和等基础知识,以及准确表述,分析和解决问题的能力.
解:
(Ⅰ)由题设得a3a4=10,且a3、a4均为非负整数,所以a3的可能的值为1,2,5,10.
若a3=1,则a4=10,a5=![]() ,与题设矛盾.
,与题设矛盾.
若a3=5,则a4=2,a5=![]() ,与题设矛盾.
,与题设矛盾.
若a3=10,则a4=1,a5=60,a6=![]() ,与题设矛盾.
,与题设矛盾.
所以a3=2.
(Ⅱ)用数学归纳法证明:
①当n=3,a3=a1+2,等式成立.
②假设当n=k(k≥3)时等式成立,即ak=ak-2+2,
由题设ak+1ak=(ak-1+2)(ak-2+2),
因为ak=ak-2+2≠0,
所以ak+1=ak-1+2,
也就是说,当n=k+1时,等式ak+1=ak-1+2成立.
根据①和②,对于所有n≥3,有an+1=an-1+2.
(Ⅲ)由a2k-1=a2(k-1)-1+2,a1=0,及
a2k=a2(k-1)+2,a2=3得a2k-1=2(k-1),a2k=2k+1,k=1,2,3,….
即an=n+(-1)n,n=1,2,3,….
所以Sn=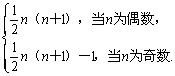

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目