题目内容
【题目】在无穷数列![]() 中,
中,![]() ,记
,记![]() 前
前![]() 项中的最大项为
项中的最大项为![]() ,最小项为
,最小项为![]() ,令
,令![]() .
.
(1)若![]() 的前
的前![]() 项和
项和![]() 满足
满足![]() .
.
①求![]() ;
;
②是否存在正整数![]() 满足
满足![]() ?若存在,请求出这样的
?若存在,请求出这样的![]() ,若不存在,请说明理由.
,若不存在,请说明理由.
(2)若数列![]() 是等比数列,求证:数列
是等比数列,求证:数列![]() 是等比数列.
是等比数列.
【答案】(1)①![]() ;②存在,
;②存在,![]() ,
,![]() 或
或![]() ;(2)证明见解析
;(2)证明见解析
【解析】
(1)①根据![]() ,先求出
,先求出![]() ,再由
,再由![]() ,求出
,求出![]() ,即可得出
,即可得出![]() ;
;
②先假设存在满足条件的正整数![]() 满足题意,得出
满足题意,得出![]() ,设
,设![]() ,研究其增减性,设
,研究其增减性,设![]() ,得
,得![]() ,设
,设![]() ,研究其增减性,进而可得出结果;
,研究其增减性,进而可得出结果;
(2)因为![]() ,且
,且![]() 、
、![]() 分别为
分别为![]() 前
前![]() 项中的最大项和最小项,所以
项中的最大项和最小项,所以![]() ,
,![]() ,设数列
,设数列![]() 的公比为
的公比为![]() ,显然
,显然![]() ,分别讨论
,分别讨论![]() ,
,![]() ,
,![]() ,三种情况,即可得出结果.
,三种情况,即可得出结果.
解:①在![]() 中,令
中,令![]() ,得
,得![]() ,解得
,解得![]() ,∴
,∴![]() ,
,
当![]() 时,
时,![]() ,
,
综上![]() .
.
显然![]() 为单调递增数列,所以
为单调递增数列,所以![]() ,
,![]() ,所以
,所以![]() .
.
②假设存在满足条件的正整数![]() ,则
,则![]() ,所以
,所以![]() ,
,
设![]() ,则
,则![]() ,所以
,所以![]() ,
,
由![]() ,得
,得![]() ,∴
,∴![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() 显然不成立,
显然不成立,
当![]() 时,
时,![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,得
,得![]() ,
,
设![]() ,则
,则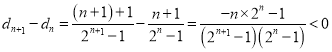 恒成立,
恒成立,
所以数列![]() 单调递减,而
单调递减,而![]() ,
,![]() ,
,![]() ,则
,则![]() 时,
时,![]() 恒成立,
恒成立,
故方程![]() 的解有且仅有
的解有且仅有![]() ,
,![]() 或
或![]() ,
,![]() ,
,
故满足条件的![]() 存在,
存在,![]() ,
,![]() 或
或![]() .
.
(2)证明:因为![]() ,且
,且![]() 、
、![]() 分别为
分别为![]() 前
前![]() 项中的最大项和最小项,
项中的最大项和最小项,
所以![]() ,
,![]() ,设数列
,设数列![]() 的公比为
的公比为![]() ,显然
,显然![]() ,
,
①当![]() 时,
时,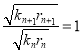 ,得
,得![]() ,
,
若![]() ,则
,则![]() ,由
,由![]() 与
与![]() 的含义可知
的含义可知![]() 与
与![]() 不可能同时成立,
不可能同时成立,
故![]() ,则
,则![]() ,则
,则![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
所以数列![]() 是等比数列.
是等比数列.
②当![]() 时,
时, ,得
,得![]() ,
,
∴![]() ,∴
,∴![]() 恒成立,而
恒成立,而![]() ,所以
,所以![]() ,∴
,∴![]() 恒成立,
恒成立,
∴![]() ,
,![]() ,代入
,代入![]() 得
得![]() ,即
,即![]() ,
,
所以数列![]() 是等比数列.
是等比数列.
③当![]() 时,
时,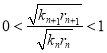 ,得
,得![]() ,
,
∴![]() ,∴
,∴![]() 恒成立,而
恒成立,而![]() ,所以
,所以![]() ,∴
,∴![]() 恒成立,
恒成立,
∴![]() ,
,![]() ,代入
,代入![]() 得
得![]() ,即
,即![]() ,
,
所以数列![]() 是等比数列.
是等比数列.
综上①②③,数列![]() 是等比数列.
是等比数列.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目