Question

7．已知f（x）=|x²-4x+3|．
（1）作出函数f（x）的图象；
（2）求函数f（x）的单调区间，并指出单调性；
（3）求集合M={m|使方程f（x）=mx有四个不相等的实根}．

Answer 1

分析 （1）借助对称性作f（x）=|x²-4x+3|的图象即可，
（2）由图象写出函数f（x）的单调区间即可；
（3）作f（x）=|x²-4x+3|与y=mx的图象，求导确定相切时直线的斜率，从而求集合M．

解答 解：（1）作f（x）=|x²-4x+3|的图象如下，
，
（2）由图象可知，
f（x）在（-∞，1），（2，3）上单调递减，
在（1，2），（3，+∞）上单调递增；
（3）作f（x）=|x²-4x+3|与y=mx的图象如下，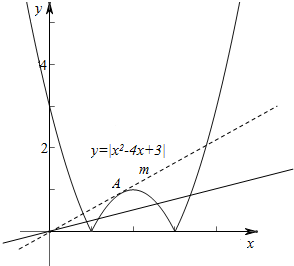
，
可知直线m与曲线相切，
当1＜x＜3时，f（x）=-（x²-4x+3），
f′（x）=-2x+4，
故-2x+4=$\frac{-{x}^{2}+4x-3}{x}$，
即x=$\sqrt{3}$，
故直线m的斜率k=4-2$\sqrt{3}$，
故集合M={m|使方程f（x）=mx有四个不相等的实根}=（0，4-2$\sqrt{3}$）．

点评 本题考查了学生的作图与应用图象的能力，同时考查了导数的综合应用．