题目内容
(09年临沭县模块考试理)(12分)
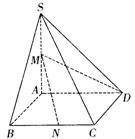
如图,在四棱锥S―ABCD中,底面ABCD是边长为1的菱形,∠ABC=![]() ,SA⊥底面
,SA⊥底面
ABCD,SA=2,M 的为SA的中点,N在线段BC上。
(Ⅰ)当![]() 为何值时,MN∥平面SCD;(说明理由)。
为何值时,MN∥平面SCD;(说明理由)。
(Ⅱ)求MD和平面SCD所成角的正弦值。
解析:(Ⅰ)法一:当![]() =
=![]() 时,MN∥平面SCD。 ????????????????1分
时,MN∥平面SCD。 ????????????????1分
证明如下:取SB中点E,连线ME,NE ????????????????2分
则ME∥AB,又∵AB∥CD
∴ME∥CD ????????????????3分
又∵NE∥SC ????????????????4分
∵ME∩NE=E
∴平面MNE∥平面SCD ????????????????5分
又MN![]() 平面MNE
平面MNE
∴MN∥平面SCD ????????????????6分
法二:作AP⊥CD于点P(如图),分别以AB、AP、AS所在直线为x、y、z轴建立空间
坐标系。

A(0,0,0),B(1,0,0),
P(0,![]() ,0),D(
,0),D(![]() ,
,![]() ,0),
,0),
S(0,0,2),M(0,0,1),
C(1![]() ,
,![]() ,0),
,0),
设![]()
∴![]() (
(![]() ,
,![]() ,0)
,0)
=![]() ?????????????????3分
?????????????????3分
![]() ?????????????????4分
?????????????????4分
设平面SCD的法向量为![]() ,则
,则
![]()
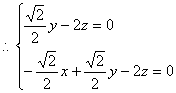
取![]() ,得
,得![]() ?????????????????5分
?????????????????5分
∵![]()
∴![]() =
=![]() ,即N为BC中点时,MN∥平面SCD ?????????????????6分
,即N为BC中点时,MN∥平面SCD ?????????????????6分
(Ⅱ)∵![]() ?????????????????7分
?????????????????7分
又∵平面SCD的法向量为![]() ?????????????????9分
?????????????????9分
∴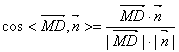 ????????????????10分
????????????????10分
=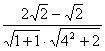 =
=![]() ????????????????11分
????????????????11分
∴MD和平面SCD所成角的正弦值为![]() ?????????????????12分
?????????????????12分

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案