题目内容
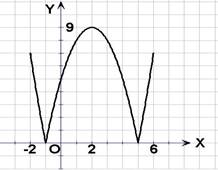
设函数![]() .(1)在区间
.(1)在区间![]() 上画出函数
上画出函数![]() 的图像;
的图像;
 (2)设集合
(2)设集合![]() . 试判断集合
. 试判断集合![]() 和
和![]() 之间的关系,并给出证明;
之间的关系,并给出证明;
(3)当![]() 时,求证:在区间
时,求证:在区间![]() 上,
上,![]() 的图像位于函数
的图像位于函数![]() 图像的上方.
图像的上方.
[解](1)如右图。
 (2)方程
(2)方程![]() 的解分别是
的解分别是![]() 和
和![]() ,由于
,由于![]() 在
在![]() 和
和![]() 上单调递减,在
上单调递减,在![]() 和
和![]() 上单调递增,因此
上单调递增,因此
![]() .
.
由于![]() .
.
(3)解:当![]() 时,
时,![]() .
.
![]()
![]()
![]() ,
,
![]()
![]() . 又
. 又![]() ,
,
① 当![]() ,即
,即![]() 时,取
时,取![]() ,
,
![]()
![]() .
.
![]() , 则
, 则![]() .
.
② 当![]() ,即
,即![]() 时,取
时,取![]() ,
, ![]() =
=![]() .
.
由 ①、②可知,当![]() 时,
时,![]() ,
,![]() .
.
因此,在区间![]() 上,
上,![]() 的图像位于函数
的图像位于函数![]() 图像的上方.
图像的上方.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
.
 上画出函数
上画出函数 的图象
;
的图象
; . 试判断集合
. 试判断集合 和
和 之间的关系,并给出证明.
之间的关系,并给出证明.  .
.
 上画出函数
上画出函数 的图象
;
的图象
; . 试判断集合
. 试判断集合 和
和 之间的关系,并给出证明.
之间的关系,并给出证明. .
. 上画出函数
上画出函数 的图象
;
的图象
; . 试判断集合
. 试判断集合 和
和 之间
之间 时,求证:在区间
时,求证:在区间 上,
上, 的图象位于函数
的图象位于函数
 .
. 上画出函数
上画出函数 的图象;
的图象; 在区间
在区间 的取值范围.
的取值范围.