题目内容
设函数 .
.
(1)在区间 上画出函数
上画出函数 的图象
;
的图象
;
(2)设集合 . 试判断集合
. 试判断集合 和
和 之间
之间
的关系,并给出证明 ;
(3)当 时,求证:在区间
时,求证:在区间 上,
上, 的图象位于函数
的图象位于函数 图象的上方.
图象的上方.

【答案】
(1)见解析;(2)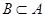 ;(3)见解析.
;(3)见解析.
【解析】
试题分析:(1)画出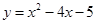 在
在 上的图象,然后将
上的图象,然后将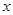 轴下方的翻到上方即可;(2)结合图象,求出集合
轴下方的翻到上方即可;(2)结合图象,求出集合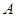 ,则其与
,则其与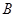 的关系一面了然;(3)只需证明
的关系一面了然;(3)只需证明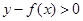 当
当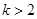 时在区间
时在区间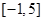 上恒成立.
上恒成立.
试题解析:(1)函数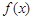 在区间
在区间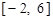 上画出的图象如下图所示:
上画出的图象如下图所示:
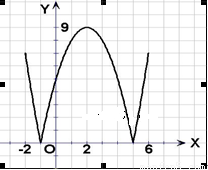
(2)方程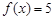 的解分别是
的解分别是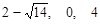 和
和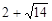 ,
,
由于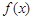 在
在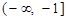 和
和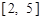 上单调递减,在
上单调递减,在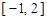 和
和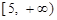 上单调递增,
上单调递增,
因此 . 6分
. 6分
由于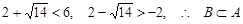 . 8分
. 8分
(3)解法一:当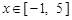 时,
时,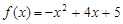 .
.
设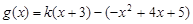
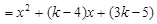
 , 9分
, 9分

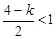 . 又
. 又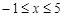 ,
,
① 当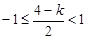 ,即
,即 时,取
时,取 ,
,
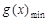
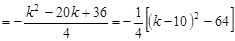 .
.
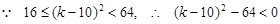 ,
则
,
则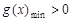 . 11分
. 11分
② 当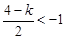 ,即
,即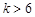 时,取
时,取 ,
,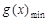 =
= .
.
由 ①、②可知,当 时,
时, ,
,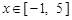 .
12分
.
12分
因此,在区间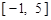 上,
上,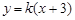 的图象位于函数
的图象位于函数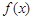 图象的上方. 13分
图象的上方. 13分
解法二:当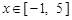 时,
时,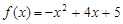 .
.
由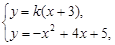 得
得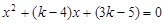 ,
,
令 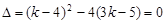 ,解得
,解得
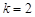 或
或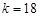 ,
10分
,
10分
在区间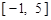 上,当
上,当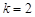 时,
时,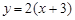 的图象与函数
的图象与函数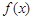 的图象只交于一点
的图象只交于一点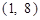 ;
;
当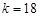 时,
时, 的图象与函数
的图象与函数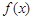 的图象没有交点.
11分
的图象没有交点.
11分
如图可知,由于直线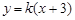 过点
过点 ,
,
当 时,直线
时,直线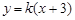 是由直线
是由直线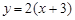 绕点
绕点 逆时针方向旋转得到.
逆时针方向旋转得到.
因此,在区间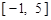 上,
上,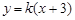 的图象位于函数
的图象位于函数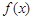 图象的上方. 13分
图象的上方. 13分
考点:1.集合间的关系;2.函数的最值求法;3.函数图象.

练习册系列答案
相关题目