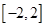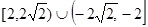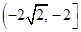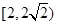题目内容
设椭圆 的离心率为
的离心率为 ,右焦点为
,右焦点为 ,方程
,方程 的两个实根分别为
的两个实根分别为 和
和 ,则点
,则点 ( )
( )
A.必在圆 内 内 | B.必在圆 上 上 |
C.必在圆 外 外 | D.以上三种情形都有可能 |
A
解析试题分析:要判断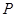 点在圆内,圆外,还是在圆上,我们只要把
点在圆内,圆外,还是在圆上,我们只要把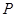 的坐标代入圆的方程,这里计算
的坐标代入圆的方程,这里计算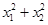 比较它与2的大小,
比较它与2的大小,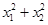
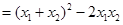 ,又由已知
,又由已知 ,
,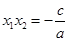 ,椭圆离心率为
,椭圆离心率为 ,从而
,从而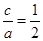 ,那么
,那么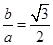 ,由此
,由此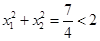 ,点在圆内.
,点在圆内.
考点:点与圆的位置关系.

练习册系列答案
相关题目
过圆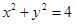 上的一点
上的一点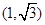 的圆的切线方程是 ( )
的圆的切线方程是 ( )
A.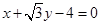 | B.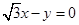 |
C.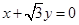 | D.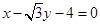 |
若点 和点
和点 到直线
到直线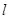 的距离依次为
的距离依次为 和
和 ,则这样的直线有( )
,则这样的直线有( )
A. 条 条 | B. 条 条 | C. 条 条 | D. 条 条 |
在平面直角坐标系内,若圆 :
: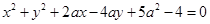 的圆心在第二象限内,则实数
的圆心在第二象限内,则实数 的取值范围为( )
的取值范围为( )
A.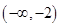 | B.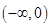 | C.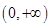 | D.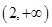 |
已知 为坐标原点,直线
为坐标原点,直线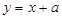 与圆
与圆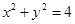 分别交于
分别交于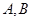 两点.若
两点.若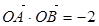 ,则实数
,则实数 的值为( )
的值为( )
| A.1 | B.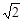 | C.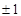 | D.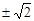 |
经过圆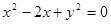 的圆心且与直线
的圆心且与直线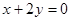 平行的直线方程是( )
平行的直线方程是( )
A.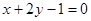 | B.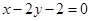 | C.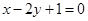 | D.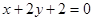 |
当直线l:y=k(x-1)+2被圆C:(x-2)2+(y-1)2=5截得的弦最短时,k的值为 ( ).
| A.2 | B.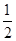 | C.3 | D.1 |
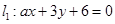 ,
,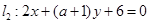 ,和圆C:
,和圆C: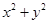
 的位置关系是“平行相交”,则b的取值范围为( )
的位置关系是“平行相交”,则b的取值范围为( )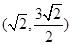
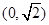
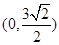

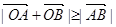 ,则实数
,则实数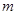 的取值范围是( )
的取值范围是( )