题目内容
过圆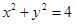 上的一点
上的一点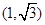 的圆的切线方程是 ( )
的圆的切线方程是 ( )
A.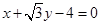 | B.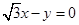 |
C.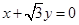 | D.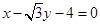 |
A
解析试题分析:圆的圆心为原点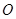
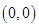 ,设切点为
,设切点为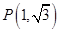 ,所以
,所以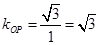 ,所以切线斜率为
,所以切线斜率为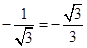 ,所以此切线方程为
,所以此切线方程为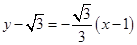 ,即
,即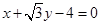 ,故A正确。
,故A正确。
考点:圆的切线方程。

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
若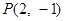 为圆
为圆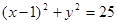 的弦
的弦 的中点,则直线
的中点,则直线 的方程是( )
的方程是( )
A.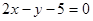 | B.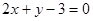 |
C.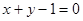 | D.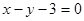 |
已知直线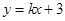 与圆
与圆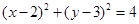 相交于
相交于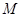 ,
,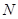 两点,若
两点,若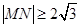 ,则
,则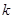 的取值范围为( )
的取值范围为( )
A.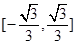 | B. |
C.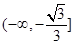 | D.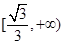 |
直线 与圆
与圆 的位置关系是( )
的位置关系是( )
| A.相离 | B.相切 | C.相交且过圆心 | D.相交但不过圆心 |
直线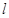 过点
过点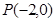 且与圆
且与圆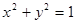 相切,则
相切,则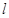 的斜率是( )
的斜率是( )
A. ; ; | B.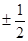 ; ; | C.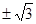 ; ; | D.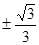 . . |
设椭圆 的离心率为
的离心率为 ,右焦点为
,右焦点为 ,方程
,方程 的两个实根分别为
的两个实根分别为 和
和 ,则点
,则点 ( )
( )
A.必在圆 内 内 | B.必在圆 上 上 |
C.必在圆 外 外 | D.以上三种情形都有可能 |
已知圆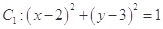 ,圆
,圆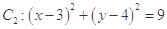 ,
,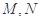 分别是圆
分别是圆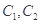 上的动点,
上的动点, 为
为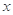 轴上的动点,则
轴上的动点,则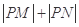 的最小值为( )
的最小值为( )
A.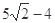 | B.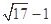 | C.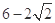 | D.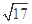 |
垂直于直线y=x+1且与圆x2+y2=1相切于第一象限的直线方程( ).
A.x+y- =0 =0 | B.x+y+1=0 |
| C.x+y-1=0 | D.x+y+ =0 =0 |
 的两条切线,切点分别为A、B,则直线AB的方程为( )
的两条切线,切点分别为A、B,则直线AB的方程为( ) B.
B.
 D.
D.