题目内容
18.已知f(x)=ex,g(x)=mx+n,若对任意实数x,都有f(x)≥g(x),则mn的最大值为$\frac{e}{2}$.分析 由题意可得f(x)-g(x)≥0恒成立,即为ex-mx-n≥0,令h(x)=ex-mx-n,求出函数的导数,再分别讨论m=0,m<0,m>0的情况,从而得出mn的最大值.
解答 解:由题意可得f(x)-g(x)≥0恒成立,即为ex-mx-n≥0,
令h(x)=ex-mx-n,h′(x)=ex-m,
若m=0,则h(x)=ex-n的最小值为h(x)>-n≥0,
得n≤0,此时mn=0;
若m<0,则h′(x)>0,函数单调增,x→-∞,此时h(x)→-∞,不可能恒有h(x)≥0.
若m>0,则得极小值点x=lnm,由h(lnm)=m-mlnm-n≥0,得n≤m(1-lnm),
mn≤m2(1-lnm)=k(m).
现求k(m)的最小值:由k′(m)=2m(1-lnm)-m=m(1-2lnm)=0,
得极小值点m=${e}^{\frac{1}{2}}$,
k(${e}^{\frac{1}{2}}$)=$\frac{e}{2}$,
所以mn的最大值为$\frac{e}{2}$,
故答案为:$\frac{e}{2}$.
点评 本题考查了函数的单调性,导数的应用,渗透了分类讨论思想,是一道综合题.

练习册系列答案
相关题目
8.已知M={x|x2+x-2>0},$N=\{x|\frac{2}{2-x}>1\}$,则M∩N=( )
| A. | {x|1<x<2} | B. | {x|0<x<1} | C. | {x|x<-2或x>1} | D. | {x|-2<x<2} |
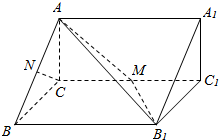 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,CC1=4,M是棱CC1的中点.
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,CC1=4,M是棱CC1的中点. 一个几何体的三视图如图所示:
一个几何体的三视图如图所示: