题目内容
9.已知边长为$\sqrt{2}$的正方形ABCD的对角线BD上任意取一点P,则$\overrightarrow{BP}$•($\overrightarrow{PA}$+$\overrightarrow{PC}$)的取值范围是$[-4,\frac{1}{2}]$.分析 如图所示,建立直角坐标系,可得A(0,0),$B(\sqrt{2},0)$,C$(\sqrt{2},\sqrt{2})$,$D(0,\sqrt{2})$.设$\overrightarrow{BP}=λ\overrightarrow{BD}$=$(-\sqrt{2}λ,\sqrt{2}λ)$,(0≤λ≤1).利用向量的坐标运算与数量积运算性质可得:$\overrightarrow{BP}$•($\overrightarrow{PA}$+$\overrightarrow{PC}$)=-8$(λ-\frac{1}{4})^{2}$+$\frac{1}{2}$=f(λ),再利用二次函数的单调性即可得出.
解答 解:如图所示,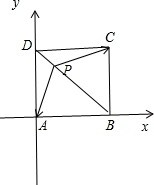
A(0,0),$B(\sqrt{2},0)$,C$(\sqrt{2},\sqrt{2})$,$D(0,\sqrt{2})$.
$\overrightarrow{BD}$=$(-\sqrt{2},\sqrt{2})$,
设$\overrightarrow{BP}=λ\overrightarrow{BD}$=$(-\sqrt{2}λ,\sqrt{2}λ)$,(0≤λ≤1).
则$\overrightarrow{OP}$=$\overrightarrow{OB}+λ\overrightarrow{BD}$=$(\sqrt{2},0)$+λ$(-\sqrt{2},\sqrt{2})$=$(\sqrt{2}-\sqrt{2}λ,\sqrt{2}λ)$.
∴$\overrightarrow{PA}$=$(\sqrt{2}λ-\sqrt{2},-\sqrt{2}λ)$,$\overrightarrow{PC}$=$(\sqrt{2}λ,\sqrt{2}-\sqrt{2}λ)$,
∴$\overrightarrow{PA}+\overrightarrow{PC}$=$(2\sqrt{2}λ-\sqrt{2},\sqrt{2}-2\sqrt{2}λ)$.
∴$\overrightarrow{BP}$•($\overrightarrow{PA}$+$\overrightarrow{PC}$)=$-\sqrt{2}λ$$(2\sqrt{2}λ-\sqrt{2})$+$\sqrt{2}λ$$(\sqrt{2}-2\sqrt{2}λ)$=-8λ2+4λ=-8$(λ-\frac{1}{4})^{2}$+$\frac{1}{2}$=f(λ),
∵0≤λ≤1,∴当$λ=\frac{1}{4}$时,f(λ)取得最大值$\frac{1}{2}$.
又f(0)=0,f(1)=-4,
∴λ=1时,f(λ)取得最小值-4.
∴f(λ)∈$[-4,\frac{1}{2}]$.
故答案为:$[-4,\frac{1}{2}]$.
点评 本题考查了向量的坐标运算与数量积运算性质、二次函数的单调性,考查了推理能力与技能数列,属于中档题.

| A. | (-$\frac{π}{2}$,$\frac{π}{2}$) | B. | (-π,-$\frac{π}{2}$) | C. | ($\frac{π}{2}$,π) | D. | ($\frac{3π}{2}$,2π) |
| A. | 一定无零点 | B. | 一定有零点 | C. | 可能有两个零点 | D. | 至多有一个零点 |
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(2)求y关于t的线性回归方程;
(3)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
$\hat b=\frac{{\sum_{i=1}^n{({t_i}-{{\overline{t}}_{\;}})({y_i}-\overline{y})}}}{{\sum_{i=1}^n{{{({t_i}-{{\overline{t}}})}^2}}}}$.$\overline{t}$.