题目内容
如图,一矩形铁皮的长为8cm,宽为5cm,在四个角上截去四个相同的小正方形,制成一个无盖的小盒子,则小正方形的边长为 时,盒子容积最大?。
1
解析试题分析:设小正方形的边长为xcm,则x∈(0,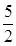 );
);
盒子容积为:y=(8-2x)•(5-2x)•x=4x3-26x2+40x,
对y求导,得y′=12x2-52x+40,令y′=0,得12x2-52x+40=0,解得:x=1,x= (舍去),
(舍去),
所以,当0<x<1时,y′>0,函数y单调递增;当1<x<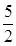 时,y′<0,函数y单调递减;
时,y′<0,函数y单调递减;
所以,当x=1时,函数y取得最大值18;
所以,小正方形的边长为1cm,盒子容积最大,最大值为18cm3..
考点:函数模型的选择与应用..

练习册系列答案
相关题目
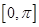 上,关于
上,关于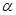 的方程
的方程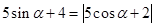 解的个数为 .
解的个数为 . 的最大值为 .
的最大值为 . 的所有零点之和为 .
的所有零点之和为 . 是
是 上的奇函数,且
上的奇函数,且 ,下面关于
,下面关于 ;
; 对称;
对称; 对称.
对称. 是首项为
是首项为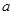 ,公差为1的等差数列,
,公差为1的等差数列, ,若对任意的
,若对任意的 ,都有
,都有 成立,则实数
成立,则实数
 的定义域是 .
的定义域是 . (K为给定常数),已知函数
(K为给定常数),已知函数 ,若对于任意的
,若对于任意的 ,恒有
,恒有 ,则实数K的取值范围为 .
,则实数K的取值范围为 .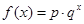 ,
, ;②
;② ;③
;③ .
. 与月份x关系的函数模型为_________(填写相应函数的序号),若所选函数满足
与月份x关系的函数模型为_________(填写相应函数的序号),若所选函数满足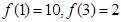 ,则
,则