题目内容
1.已知圆x2+y2-6mx-2(m-1)y+10m2-2m-24=0(m∈R).(1)求证:不论m为何值,圆心在同一直线l上;
(2)与l平行的直线中,哪些与圆相交、相切、相离;
(3)求证:任何一条平行于l且与圆相交的直线被各圆截得的弦长相等.
分析 (1)将圆的方程化为标准方程,可得圆心坐标,再消去参数,即可得到结论;
(2)设与l平行的直线是l1:x-3y+b=0,求出圆心到直线l1的距离,与半径比较,即可得出结论;
(3)设出与直线?平行的直线的方程:x-3y+b=0,利用点到直线的距离公式表示出圆心到此直线的距离整理后发现不含有参数b,故可得结论.
解答 (1)证明:配方得:(x-3m)2+[y-(m-1)]2=25,设圆心为(x,y),
则$\left\{\begin{array}{l}{x=3m}\\{y=m-1}\end{array}\right.$,
消去m得x-3y-3=0,则圆心恒在直线l:x-3y-3=0上.
(2)解:设与l平行的直线是l1:x-3y+b=0,
则圆心到直线l1的距离为d=$\frac{|3m-3(m-1)+b|}{\sqrt{10}}$=$\frac{|3+b|}{\sqrt{10}}$.
∵圆的半径为r=5,
∴当d<r,即-5$\sqrt{10}$-3<b<5$\sqrt{10}$-3时,直线与圆相交;
当d=r,即b=±5$\sqrt{10}$-3时,直线与圆相切;
当d>r,即b<-5$\sqrt{10}$-3或b>5$\sqrt{10}$-3时,直线与圆相离.
(3)证明:对于任一条平行于l且与圆相交的直线l1:x-3y+b=0,由于圆心到直线l1的距离d=$\frac{|3+b|}{\sqrt{10}}$,
弦长=2$\sqrt{{r}^{2}}-{d}^{2}$且r和d均为常量.
∴任何一条平行于l且与圆相交的直线被各圆截得的弦长相等.
点评 本题考查直线与圆的方程的应用,考查弦长的计算,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列推理错误的是( )
| A. | A∈l,A∈α,B∈l,B∈α⇒l?α | B. | A∈α,A∈β,B∈α,B∈β⇒α∩β=AB | ||
| C. | l?α,A∈l⇒A∉α | D. | A∈l,l?α⇒A∈α |
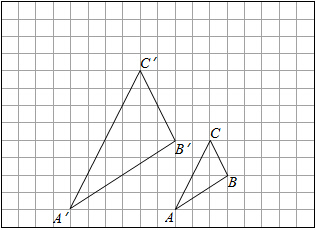 如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.