题目内容
已知三棱锥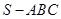 的所有顶点都在球
的所有顶点都在球 的球面上,
的球面上, 是边长为
是边长为 的正三角形,
的正三角形, 为球
为球 的直径,且
的直径,且 ,则此棱锥的体积为( )
,则此棱锥的体积为( )
A. | B. | C. | D.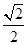 |
A
解析试题分析:取AB的中点D,连接SD,ED,作SE⊥EC,则AB⊥SD,AB⊥CD,所以AB⊥面SDC,因为  为球
为球 的直径,且
的直径,且 ,所以∠SBAC=∠SAC=900,所以SA=SB=
,所以∠SBAC=∠SAC=900,所以SA=SB= ,所以
,所以 ,
, ,在三角形SDC中,
,在三角形SDC中, ,
,
所以 ,所以棱锥的体积
,所以棱锥的体积 。
。
考点:棱锥的体积公式;三棱锥的外接球。
点评:求椎体的体积,要适当的选择底面和高。做本题的关键是是把棱锥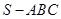 的体积转化为
的体积转化为 。此题的难度较大。考查了学生分析问题,解决问题的能力。同时也考查了学生的空间想象能力。
。此题的难度较大。考查了学生分析问题,解决问题的能力。同时也考查了学生的空间想象能力。

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
一个与球心距离为1的平面截球所得的圆面积为 ,则球的表面积为( )
,则球的表面积为( )
A. | B. | C. | D. |
某多面体的三视图(单位:cm)如图所示,则此多面体的体积是( )
A. | B.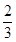 cm3 cm3 | C. cm3 cm3 | D.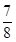 cm3 cm3 |
设有一几何体的三视图如下,则该几何体体积为( )

正视图 侧视图
俯视图(圆和正方形)
A.4+ | B.4+ | C.4+ | D.4+ |
如图,三棱柱A1B1C1—ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( ).
| A.AE、B1C1为异面直线,且AE⊥B1C1 |
| B.AC⊥平面A1B1BA |
| C.CC1与B1E是异面直线 |
| D.A1C1∥平面AB1E |
已知a、b是异面直线,直线c//a,那么c与b ( )
| A.一定是异面直线 | B.一定是相交直线 |
| C.不可能是相交直线 | D.不可能是平行直线 |
一个棱锥的三视图如图,则该棱锥的全面积(单位:cm2)为( ) 
A.36+12 | B.48+24 | C.48+12 | D.36+24 |
 与
与 是异面直线的是 ……………………………………………( )
是异面直线的是 ……………………………………………( )