题目内容
【题目】如图所示，已知点
，过点
作直线
、
与圆
：
和抛物线
：
都相切.
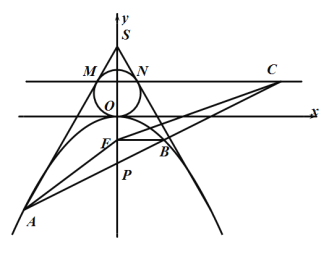
（1）求抛物线的两切线的方程；
（2）设抛物线的焦点为
，过点
的直线与抛物线相交于
、
两点，与抛物线的准线交于点（其中点靠近点），且
，求
与
的面积之比.
【答案】（1）
；（2）面积比
.
【解析】
（1）设过点
的直线，利用直线与圆相切的性质、结合点到直线的距离公式，最后求出切线方程；
（2）由（1）可知圆的切线与抛物线也相切，利用方程思想可以求出抛物线的标准方程，利用抛物线的定义可以求出
点坐标，进而可以求出
、
两点坐标，最后求出面积比即可.
（1）设过点的直线方程为：
，圆
：
的圆心为
，半径为1，该直线与圆相切，所以有：
，因此圆的切线方程为
，即两条切线方程分别为：；
（2）由（1）可知：直线与
相切，
所以方程
的判别式为零，
即
，所以抛物线的方程为：
，准线方程为：
，设点坐标为：
，因为
，所以由抛物线的定义可知：
，因此可得
，而靠近点，所以点为
，直线
的方程为：
，所以
或
，因此点坐标为
，直线与抛物线的准线交于点，所以
，点坐标为
，
与
的面积之比为：
，所以它们的面积比为：2:5.
练习册系列答案
相关题目
【题目】随着移动互联网的发展，与餐饮美食相关的手机
软件层出不穷.为调查某款订餐软件的商家的服务情况，统计了10次订餐“送达时间”，得到茎叶图如下：（时间：分钟）
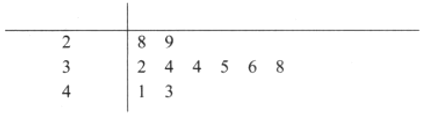
（1）请计算“送达时间”的平均数与方差：
（2）根据茎叶图填写下表：
送达时间 | 35分组以内（包括35分钟） | 超过35分钟 |
频数 | A | B |
频率 | C | D |
在答题卡上写出
，
，
，
的值；
（3）在（2）的情况下，以频率代替概率.现有3个客户应用此软件订餐，求出在35分钟以内（包括35分钟）收到餐品的人数
的分布列，并求出数学期望.
