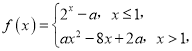题目内容
【题目】2018年高考成绩揭晓,某高中再创辉煌,考后学校对于单科成绩逐个进行分析:现对甲、乙两个文科班的数学成绩进行分析,规定:大于等于135分为优秀,135分以下为非优秀,成绩统计后,得到如下的![]() 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为![]() .
.
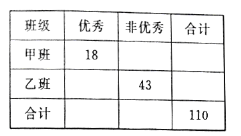
(1)请完成上面的列联表;
(2)请问:是否有75%的把握认为“数学成绩与所在的班级有关系”?
(3)用分层抽样的方法从甲、乙两个文科班的数学成绩优秀的学生中抽取5名学生进行调研,然后再从这5名学生中随机抽取2名学生进行谈话,求抽到的2名学生中至少有1名乙班学生的概率.
参考公式:![]() (其中
(其中![]() )
)
参考数据:

【答案】(1)见解析(2)有(3)![]()
【解析】分析:⑴利用已知条件直接填写联列表即可
⑵求出![]() ,即可判断结果
,即可判断结果
⑶从甲班成绩优秀的学生中抽取![]() 名,分别记为
名,分别记为![]() ,从乙班成绩优秀的学生中抽取
,从乙班成绩优秀的学生中抽取![]() 名,分别记为
名,分别记为![]() ,列出所有基本事件,设“抽到的
,列出所有基本事件,设“抽到的![]() 名学生中至少有
名学生中至少有![]() 名乙班学生”为事件
名乙班学生”为事件![]() ,求出事件
,求出事件![]() 包含的基本事件个数,然后求解概率
包含的基本事件个数,然后求解概率
详解:(1)
班级 | 优秀 | 非优秀 | 合计 |
甲班 | 37 | 55 | |
乙班 | 12 | 55 | |
合计 | 30 | 80 |
(2)由题意得![]()
所以有75%的把握认为“数学成绩与所在的班级有关系”
(3)因为甲、乙两个班数学成绩优秀的学生人数的比例为![]() ,所以从甲班成绩优秀的学生中抽取3名,
,所以从甲班成绩优秀的学生中抽取3名,
分别记为![]() ,从乙班成绩优秀的学生中抽取2名,分别记为
,从乙班成绩优秀的学生中抽取2名,分别记为![]() ,
,
则从抽取的5名学生中随机抽取2名学生的所有基本事件有![]() ,
,![]() ,共10个
,共10个
设“抽到的2名学生中至少有1名乙班学生”为事件![]() ,则事件
,则事件![]() 包含的基本事件有
包含的基本事件有![]()
![]() ,共7个,
,共7个,
所以![]() ,
,
即抽到的2名学生中至少有1名乙班学生的概率是![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目