题目内容
将一块圆心角为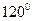 ,半径为
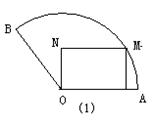
,半径为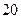 ㎝的扇形铁片裁成一块矩形,有如图(1)、(2)的两种裁法:让矩形一边在扇形的一条半径OA上,或让矩形一边与弦AB平行,请问哪 种裁法能得到最大面积的矩形?并求出这个最大值.
㎝的扇形铁片裁成一块矩形,有如图(1)、(2)的两种裁法:让矩形一边在扇形的一条半径OA上,或让矩形一边与弦AB平行,请问哪 种裁法能得到最大面积的矩形?并求出这个最大值.

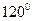 ,半径为
,半径为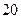 ㎝的扇形铁片裁成一块矩形,有如图(1)、(2)的两种裁法:让矩形一边在扇形的一条半径OA上,或让矩形一边与弦AB平行,请问哪 种裁法能得到最大面积的矩形?并求出这个最大值.
㎝的扇形铁片裁成一块矩形,有如图(1)、(2)的两种裁法:让矩形一边在扇形的一条半径OA上,或让矩形一边与弦AB平行,请问哪 种裁法能得到最大面积的矩形?并求出这个最大值.

最大面积为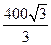
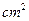
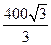
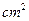
按图(1)的裁法:矩形的一边OP在OA上,顶点M在圆弧上,设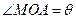 ,则
,则
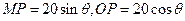 ,所以矩形OPMN的面积
,所以矩形OPMN的面积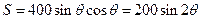
即当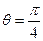 时,
时,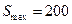 .
.
按图(2)的裁法:矩形一边PQ与弦AB平行,设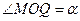 ,在△MOQ中,
,在△MOQ中,
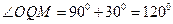 ,则正弦定理得:
,则正弦定理得: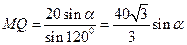
又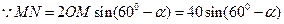
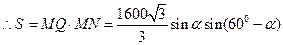

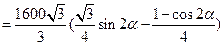

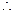 当
当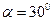 时,
时,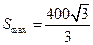
由于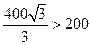 ,所以用第二种裁法得面积最大的矩形,最大面积为
,所以用第二种裁法得面积最大的矩形,最大面积为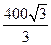
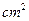 .
.
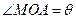 ,则
,则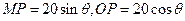 ,所以矩形OPMN的面积
,所以矩形OPMN的面积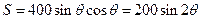
即当
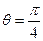 时,
时,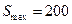 .
.按图(2)的裁法:矩形一边PQ与弦AB平行,设
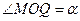 ,在△MOQ中,
,在△MOQ中,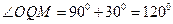 ,则正弦定理得:
,则正弦定理得: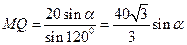
又
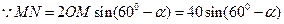
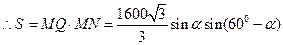

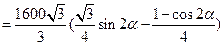

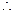 当
当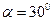 时,
时,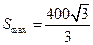
由于
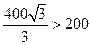 ,所以用第二种裁法得面积最大的矩形,最大面积为
,所以用第二种裁法得面积最大的矩形,最大面积为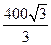
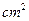 .
.
练习册系列答案
相关题目
 的图象 如图所示,则
的图象 如图所示,则 的值等于 .
的值等于 . 
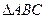 中,角
中,角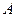 、
、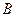 、
、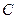 的对边分别为
的对边分别为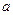 、
、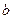 、
、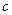 ,且
,且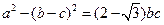 ,
,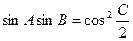 ,
,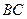 边上中线
边上中线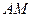 的长为
的长为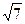 .
.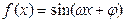
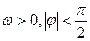 ),
),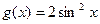 .若函数
.若函数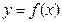 的图像与x轴的任意两个相邻交点间的距离为
的图像与x轴的任意两个相邻交点间的距离为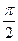 ,且直线
,且直线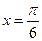 是函数
是函数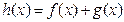 的单调递增区间.
的单调递增区间.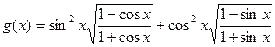 ,其中
,其中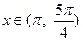 ,求函数
,求函数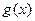 的值域.
的值域.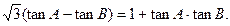
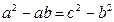 ,求A、B、C的大小;
,求A、B、C的大小;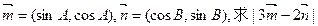 的取值范围.
的取值范围.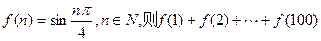 =____________.
=____________.
 ,则
,则 .
.