题目内容
如图,二面角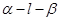 的大小是60°,线段
的大小是60°,线段 .
.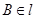 ,AB与
,AB与 所成的角为30°.则AB与平面
所成的角为30°.则AB与平面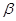 所成的角的正弦值是 .
所成的角的正弦值是 .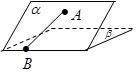
 .
.
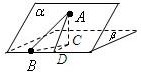
解析试题分析:过点A作平面β的垂线,垂足为C,
在β内过C作l的垂线.垂足为D,
连接AD,有三垂线定理可知AD⊥l,
故∠ADC为二面角α-l-β的平面角,为60°,
又由已知,∠ABD=30°,
连接CB,则∠ABC为AB与平面β所成的角
设AD=2,则AC=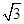 ,CD=1
,CD=1
AB=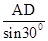 =4
=4
∴sin∠ABC=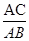 =
= ;
;
故答案为 。
。
考点:本题主要考查二面角的计算。
点评:基础题,本解法反映了求二面角方法的“几何法”—“一作、二证、三计算”。

练习册系列答案
相关题目
 附近,那么点A和点C到直线BD的距离之比约为
附近,那么点A和点C到直线BD的距离之比约为 
 为使互不重合的平面,
为使互不重合的平面, 是互不重合的直线,给出下列四个命题:
是互不重合的直线,给出下列四个命题:
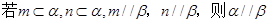
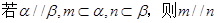
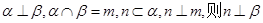 ;
; 
 与CC1所成的角;②三棱锥A1-ABD是正三棱锥;③CE⊥平面BB1D1D;④
与CC1所成的角;②三棱锥A1-ABD是正三棱锥;③CE⊥平面BB1D1D;④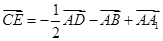 ;⑤|
;⑤| |=
|= .其中正确的命题有_____________.(写出所有正确命题的序号)
.其中正确的命题有_____________.(写出所有正确命题的序号)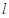 ⊥平面
⊥平面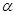 ,直线m
,直线m 平面
平面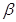 ,有下列命题:
,有下列命题: ∥
∥
 ∥m;
∥m; 的二面角内的一个球与二面角的两个面的切点到棱的距离都是6,则这个球的半径为_______.
的二面角内的一个球与二面角的两个面的切点到棱的距离都是6,则这个球的半径为_______.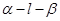 中,
中,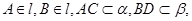 且
且 已知
已知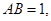
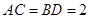 ,
, 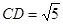 , 则二面角
, 则二面角