题目内容
若关于x的方程|x2-a|=2有且只有两个实根,则实数a的取值范围是
(-2,2)
(-2,2)
.分析:若方程|x2-a|=2有且只有两个实根,则f(x)=|x2-a|与y=2有且只有两个实根,,分a≤0,a>0两种情况分别作出函数f(x)的图象,结合图象可求a的范围
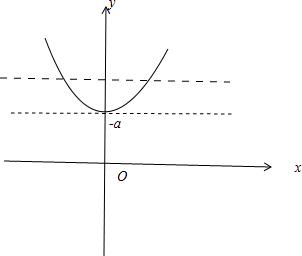
解答:解:当a≤0时,令f(x)=|x2-a|=x2-a,其图象 如图所示
要使函数f(x)与y=2有两个交点,则-a<2
∴-2<a≤0
当a>0时,令f(x)=|x2-a|=
,其图象如下图所示

要使得 f(x)与y=2有两个交点,根据函数的图象可得,a<2
∴0<a<2
综上可得,-2<a<2
故答案为:(-2,2)
要使函数f(x)与y=2有两个交点,则-a<2
∴-2<a≤0

当a>0时,令f(x)=|x2-a|=
|

要使得 f(x)与y=2有两个交点,根据函数的图象可得,a<2
∴0<a<2
综上可得,-2<a<2
故答案为:(-2,2)
点评:本题主要考查了由方程的根的个数求解参数的取值范围,转化为函数的 交点个数的应用,解答本题的关键是准确作出函数的图象,结合函数的图象进行求解,体现了数形结合思想的应用

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
△ABC中三个内角为A、B、C,若关于x的方程x2-xcosAcosB-cos2
=0有一根为1,则△ABC一定是( )
| C |
| 2 |
| A、直角三角形 |
| B、等腰三角形 |
| C、锐角三角形 |
| D、钝角三角形 |