题目内容
若关于x的方程x2-4|x|+5=m有四个不同的实数解,则实数m的取值范围是( )
分析:根据题意可以令f(x)=x2-4|x|+5,h(x)=m,可以分别画出这两个函数的图象,利用数形结合的方法进行求解;
解答:解:∵关于x的方程x2-4|x|+5=m有四个不同的实数解,
∴令f(x)=|x|2-4|x|+5=(|x|+2)2+1,h(x)=m,
分别画出函数f(x)和h(x)的图象,
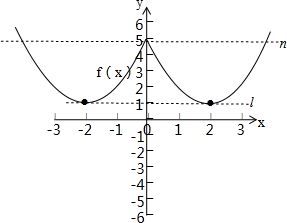
∵要使f(x)的图象与h(x)的图象有两个交点,
如上图直线h(x)=m应该在直线l和直线n之间,
∴1<m<5,
故选C.
∴令f(x)=|x|2-4|x|+5=(|x|+2)2+1,h(x)=m,
分别画出函数f(x)和h(x)的图象,

∵要使f(x)的图象与h(x)的图象有两个交点,
如上图直线h(x)=m应该在直线l和直线n之间,
∴1<m<5,
故选C.
点评:本题考查了一元二次方程根的判别式的应用,也涉及了绝对值方程的应用,利用数形结合的方法进行求解,就会比较简单;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
△ABC中三个内角为A、B、C,若关于x的方程x2-xcosAcosB-cos2
=0有一根为1,则△ABC一定是( )
| C |
| 2 |
| A、直角三角形 |
| B、等腰三角形 |
| C、锐角三角形 |
| D、钝角三角形 |