题目内容
7、若关于x的方程x2+（2-m2）x+2m=0的两根一个比1大一个比1小，则m的范围是
m＞3或m＜-1
．分析：本题宜用相关函数的图象进行转化，令f（x）=x2+（2-m2）x+2m，作出其图象，从图象上可心看出只要f（1）＜0，即可保证x的方程x2+（2-m2）x+2m=0的两根一个比1大一个比1小．
解答：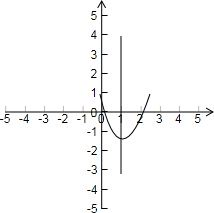
解：令f（x）=x2+（2-m2）x+2m，由题意，其图象应为
故有f（1）＜0，即1+2-m2+2m＜0
整理得m2-2m-3＞0
解得m＞3或m＜-1
故答案为m＞3或m＜-1
解：令f（x）=x2+（2-m2）x+2m，由题意，其图象应为故有f（1）＜0，即1+2-m2+2m＜0
整理得m2-2m-3＞0
解得m＞3或m＜-1
故答案为m＞3或m＜-1
点评：本题考点是一元二次方程根的分布与系数的关系，本题根据题设条件作出图象与图象找出问题的等价条件，用图象法转化是解决本题最好的方式．
练习册系列答案
阅读快车系列答案
相关题目
△ABC中三个内角为A、B、C，若关于x的方程x2-xcosAcosB-cos2
=0有一根为1，则△ABC一定是（ ）
| C |
| 2 |
| A、直角三角形 |
| B、等腰三角形 |
| C、锐角三角形 |
| D、钝角三角形 |