Question

【题目】已知抛物线E：的准线为，焦点为，为坐标原点。

（1）求过点、，且与相切的圆的方程；

（2）过点的直线交抛物线E于两点，点A关于x轴的对称点为，且点与点不重合，求证：直线过定点.

Answer 1

【答案】（1）（2）详见解析

【解析】

（1）由题意求得焦点及准线方程，即可求得圆心，利用点到直线的距离公式，即可求得半径，即可求得圆的方程；

（2）设直线AB方程为y＝k（x﹣1），代入椭圆方程，利用韦达定理，求得直线BA′的方程为，当y＝0，求得x＝﹣1，则直线BA′过定点（﹣1，0）；

（1）抛物线E：y2＝4x的准线l的方程为：x＝﹣1，焦点坐标为F（1，0），

设所求圆的圆心C（a，b），半径为r，∵圆C过O，F，

∴，∵圆C与直线l：x＝﹣1相切，

∴．

由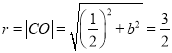，得．

∴过O，F，且与直线l相切的圆的方程为；

（2）依题意知直线AB的斜率存在，设直线AB方程为y＝k（x﹣1），A（x1，y1），B（x2，y2），（x1≠x2），A′（x1，﹣y1），

联立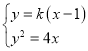，消去y得k2x2﹣（2k2+4）x+k2＝0．

∴，x1x2＝1．

∵直线BA′的方程为，又由对称性可知：定点在x轴上，

∴令y＝0，得．

直线BA′过定点（﹣1，0），