题目内容
17．设全集U=R，A={x|-1≤x＜5}，B={x|2x＞1}，C={x|x＜a}．（1）求A∪B；
（2）（CRA）∩B；
（3Ⅲ）如果A∩C≠∅，求a的取值范围．
分析 （1）根据指数函数的单调性可求出B={x|x＞0}，然后进行并集的运算即可；
（2）进行补集、交集的运算即可；
（3）A∩C≠∅，即集合A，C有公共元素，从而得到a＞-1，即求出了a的取值范围．
解答 解：（1）B={x|x＞0}；
∴A∪B={x|0＜x＜5}；
（2）∁RA={x|x＜-1，或x≥5}；
∴（∁RA）∩B={x|x≥5}；
（3）A∩C≠∅；
∴a＞-1；
∴a的取值范围为（-1，+∞）．
点评 考查描述法表示集合，指数函数的单调性，集合的交集、并集，及补集的运算，空集的概念．
练习册系列答案
名校课堂系列答案
相关题目
如图，四棱锥S-ABCD的侧倰均相等，底面ABCD为平行四边形，其对角线交点为O．
12．下列各区间的数轴表示中，正确的是（ ）
| A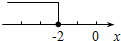． |  [-2，+∞） | B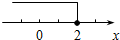． |  （-∞，2） | C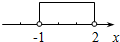． |  （-1，2） | D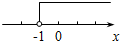． |  [-1，+∞） |
2．计算log${\;}_{\sqrt{2}}$（2$\sqrt{2}$）-log${\;}_{（\sqrt{2}-1）}$（3-2$\sqrt{2}$）+eln2的值为（ ）
| A． | 3 | B． | 2 | C． | 1 | D． | 0 |
6．不等式|2x-1|≤3的整数解组成的集合为（ ）
| A． | {0，1} | B． | {-1，0，1} | C． | {-1，0，1，2} | D． | {0，1，2} |