题目内容
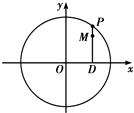 如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的射影,M为PD上一点,且|MD|=
如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的射影,M为PD上一点,且|MD|=| 4 |
| 5 |
(Ⅰ)当P在圆上运动时,求点M的轨迹C的方程
(Ⅱ)求过点(3,0)且斜率
| 4 |
| 5 |
分析:(Ⅰ)由题意P是圆x2+y2=25上的动点,点D是P在x轴上的射影,M为PD上一点,且|MD|=
|PD|,利用相关点法即可求轨迹;
(Ⅱ)由题意写出直线方程与曲线C的方程进行联立,利用根与系数的关系得到线段长度.
| 4 |
| 5 |
(Ⅱ)由题意写出直线方程与曲线C的方程进行联立,利用根与系数的关系得到线段长度.
解答:解:(Ⅰ)设M的坐标为(x,y)P的坐标为(xp,yp)
由已知得:
∵P在圆上,
∴x2+(
y)2=25,即C的方程为
+
=1.
(Ⅱ)过点(3,0)且斜率为
的直线方程为:y=
(x-3),
设直线与C的交点为A(x1,y1)B(x2,y2),
将直线方程y=
(x-3)代入C的方程,得
+
=1 即:x2-3x-8=0 ∴x1=
,x2=
,
∴线段AB的长度为|AB|=
=
=
=
.
由已知得:
|
∵P在圆上,
∴x2+(
| 5 |
| 4 |
| x2 |
| 25 |
| y2 |
| 16 |
(Ⅱ)过点(3,0)且斜率为
| 4 |
| 5 |
| 4 |
| 5 |
设直线与C的交点为A(x1,y1)B(x2,y2),
将直线方程y=
| 4 |
| 5 |
| x2 |
| 25 |
| (x-3)2 |
| 25 |
3-
| ||
| 2 |
3+
| ||
| 2 |
∴线段AB的长度为|AB|=
| (x1-x2)2+(y1-y2)2 |
(1+
|
=
|
| 41 |
| 5 |
点评:此题重点考查了利用相关点法求动点的轨迹方程,还考查了联立直线方程与曲线方程进行整体代入,还有两点间的距离公式.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
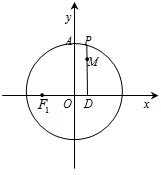 如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影,M为线段PD上一点,|PD|=
如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影,M为线段PD上一点,|PD|=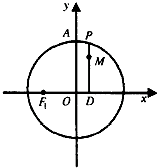 如图,设P是圆x2+y2=2上的动点,PD⊥x轴,垂足为D,M为线段PD上一点,且|PD|=
如图,设P是圆x2+y2=2上的动点,PD⊥x轴,垂足为D,M为线段PD上一点,且|PD|= (2012•茂名一模)如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影.M为线段PD上一点,且
(2012•茂名一模)如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影.M为线段PD上一点,且