题目内容
如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的射影,M为PD上一点,且|MD|=
|PD|
(1)求:当P在圆上运动时,求点M的轨迹C的方程.
(2)直线l:kx+y-5=0恒与点M的轨迹C有交点,求k的取值范围.
| 4 | 5 |
(1)求:当P在圆上运动时,求点M的轨迹C的方程.
(2)直线l:kx+y-5=0恒与点M的轨迹C有交点,求k的取值范围.
分析:(1)分别设出M和P点的坐标,利用|MD|=
|PD|求得两点坐标的关系,把P点坐标代入圆的方程化简即可得到点M的轨迹C的方程;
(2)直接联立直线方程和椭圆方程,由判别式大于等于0求解k的取值范围.
| 4 |
| 5 |
(2)直接联立直线方程和椭圆方程,由判别式大于等于0求解k的取值范围.
解答: 解:(1)如图,设M的坐标为(x,y),P的坐标为(xP,yP)
解:(1)如图,设M的坐标为(x,y),P的坐标为(xP,yP)
由已知得
.
∵P在圆上,∴x2+(
y)2=25,
即C的方程为
+
=1;
(2)联立
,得(16+25k2)x2-250kx+225=0,
利用判别式△≥0,得(-150k)2-4×225×(16+25k2)≥0.
解得k≤-
或k≥
.
∴k的取值范围是k≤-
或k≥
..
 解:(1)如图,设M的坐标为(x,y),P的坐标为(xP,yP)
解:(1)如图,设M的坐标为(x,y),P的坐标为(xP,yP)由已知得
|
∵P在圆上,∴x2+(
| 5 |
| 4 |
即C的方程为
| x2 |
| 25 |
| y2 |
| 16 |
(2)联立
|
利用判别式△≥0,得(-150k)2-4×225×(16+25k2)≥0.
解得k≤-
| 3 |
| 5 |
| 3 |
| 5 |
∴k的取值范围是k≤-
| 3 |
| 5 |
| 3 |
| 5 |
点评:本题考查了代入法求曲线的轨迹方程,考查了直线和圆锥曲线的关系,训练了判别式法判断两曲线的关系,是中档题.

练习册系列答案
相关题目
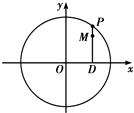 如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的射影,M为PD上一点,且|MD|=
如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的射影,M为PD上一点,且|MD|=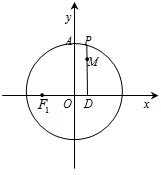 如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影,M为线段PD上一点,|PD|=
如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影,M为线段PD上一点,|PD|=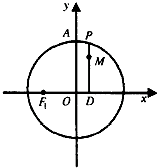 如图,设P是圆x2+y2=2上的动点,PD⊥x轴,垂足为D,M为线段PD上一点,且|PD|=
如图,设P是圆x2+y2=2上的动点,PD⊥x轴,垂足为D,M为线段PD上一点,且|PD|= (2012•茂名一模)如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影.M为线段PD上一点,且
(2012•茂名一模)如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影.M为线段PD上一点,且