题目内容
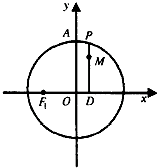 如图,设P是圆x2+y2=2上的动点,PD⊥x轴,垂足为D,M为线段PD上一点,且|PD|=
如图,设P是圆x2+y2=2上的动点,PD⊥x轴,垂足为D,M为线段PD上一点,且|PD|=| 2 |
| 2 |
(1)求点M的轨迹方程;
(2)求|MA|+|MF1|的最大值,并求此时点M的坐标.
分析:(1)确定M、P坐标之间的关系,利用P是圆x2+y2=2上的动点,即可求轨迹;
(2)由(1)知,M的轨迹方程是椭圆,F1是左焦点,设右焦点为F2,利用|MA|+|MF1|=2
+|MA|-|MF2|≤2
+|AF2|=2
+
,即可求得结论.
(2)由(1)知,M的轨迹方程是椭圆,F1是左焦点,设右焦点为F2,利用|MA|+|MF1|=2
| 2 |
| 2 |
| 2 |
| 3 |
解答:解:(1)设M的坐标为(x,y),P的坐标为(xp,yp)
∵PD⊥x轴,垂足为D,M为线段PD上一点,且|PD|=
|MD|,
∴xp=x,yp=
y
∵P是圆x2+y2=2上的动点,
∴x2+2y2=2;
(2)由(1)知,M的轨迹方程是椭圆,F1是左焦点,设右焦点为F2,坐标为(1,0)
∴|MA|+|MF1|=2
+|MA|-|MF2|≤2
+|AF2|=2
+
当A,F2,M三点共线,且M在AF2延长线上时,取等号
直线AF2的方程为x+
=1,与椭圆方程联立,解得x=
,y=
∴所求最大值为2
+
,此时M的坐标为(
,
).
∵PD⊥x轴,垂足为D,M为线段PD上一点,且|PD|=
| 2 |
∴xp=x,yp=
| 2 |
∵P是圆x2+y2=2上的动点,
∴x2+2y2=2;
(2)由(1)知,M的轨迹方程是椭圆,F1是左焦点,设右焦点为F2,坐标为(1,0)
∴|MA|+|MF1|=2
| 2 |
| 2 |
| 2 |
| 3 |
当A,F2,M三点共线,且M在AF2延长线上时,取等号
直线AF2的方程为x+
| y | ||
|
4+
| ||
| 5 |
| ||||
| 5 |
∴所求最大值为2
| 2 |
| 3 |
4+
| ||
| 5 |
| ||||
| 5 |
点评:本题考查利用相关点法求动点的轨迹方程,考查最值问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
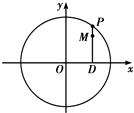 如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的射影,M为PD上一点,且|MD|=
如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的射影,M为PD上一点,且|MD|=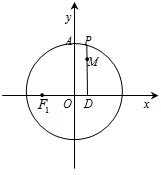 如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影,M为线段PD上一点,|PD|=
如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影,M为线段PD上一点,|PD|= (2012•茂名一模)如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影.M为线段PD上一点,且
(2012•茂名一模)如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影.M为线段PD上一点,且