题目内容
 (2012•茂名一模)如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影.M为线段PD上一点,且|MD|=
(2012•茂名一模)如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影.M为线段PD上一点,且|MD|=
| ||
| 2 |
(1)当点P在圆上运动时,求点M的轨迹C的方程;
(2)已知点F1(-1,0),F2(1,0),设点A(1,m)(m>0)是轨迹C上的一点,求∠F1AF2的平分线l所在直线的方程.
分析:(1)由题意P是圆x2+y2=25上的动点,点D是P在x轴上的摄影,M为PD上一点,且|MD|=
|PD|,利用相关点法即可求轨迹;
(2)求出A的坐标,及∠F1AF2的平分线l所在直线与x轴的交点坐标,从而可得直线的斜率,进而可得直线的方程.
| ||
| 2 |
(2)求出A的坐标,及∠F1AF2的平分线l所在直线与x轴的交点坐标,从而可得直线的斜率,进而可得直线的方程.
解答:解:(1)设M的坐标为(x,y),P的坐标为(xp,yp)
由已知|MD|=
|PD|得:xp=x,yp=
y
∵P是圆x2+y2=2上的动点,
∴x2+2y2=2;
(2)∵点A(1,m)(m>0)是轨迹C上的一点,∴1+2m2=2,∴m=
设∠F1AF2的平分线l所在直线交x轴于(a,0),则利用角平分线的性质可得
=
,∴a=
∴∠F1AF2的平分线l所在直线的斜率为
∴∠F1AF2的平分线l所在直线的方程为y-
=
(x-1),即2x-
y-1=0
由已知|MD|=
| ||
| 2 |
| 2 |
∵P是圆x2+y2=2上的动点,
∴x2+2y2=2;
(2)∵点A(1,m)(m>0)是轨迹C上的一点,∴1+2m2=2,∴m=
| ||
| 2 |
设∠F1AF2的平分线l所在直线交x轴于(a,0),则利用角平分线的性质可得
| ||||
|
| a+1 |
| 1-a |
| 1 |
| 2 |
∴∠F1AF2的平分线l所在直线的斜率为
| 2 |
∴∠F1AF2的平分线l所在直线的方程为y-
| ||
| 2 |
| 2 |
| 2 |
点评:本题考查利用相关点法求动点的轨迹方程,考查求直线方程,属于中档题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 (2012•茂名一模)如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
(2012•茂名一模)如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题: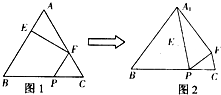 (2012•茂名一模)如图1,在正三角形ABC中,AB=3,E、F、P分别是AB、AC、BC边上的点,AE=CF=CP=1.将△AFE沿折起到△A1EF的位置,使平面A1EF与平面BCFE垂直,连接A1B、A1P(如图2).
(2012•茂名一模)如图1,在正三角形ABC中,AB=3,E、F、P分别是AB、AC、BC边上的点,AE=CF=CP=1.将△AFE沿折起到△A1EF的位置,使平面A1EF与平面BCFE垂直,连接A1B、A1P(如图2).