题目内容
已知椭圆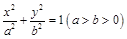 上一点
上一点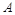 关于原点的对称点为
关于原点的对称点为 为其右焦点,若
为其右焦点,若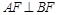 ,设
,设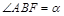 ,且
,且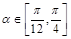 ,则该椭圆离心率的取值范围为 .
,则该椭圆离心率的取值范围为 .
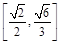
解析试题分析:∵B和A关于原点对称,∴B也在椭圆上。
设左焦点为F′,根据椭圆定义:|AF|+|AF′|=2a
又∵|BF|=|AF′| ∴|AF|+|BF|=2a ……①
O是Rt△ABF的斜边中点,∴|AB|=2c
又|AF|=2csinα ……②
|BF|=2ccosα ……③
将②③代入① 2csinα+2ccosα=2a
∴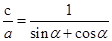 ,即
,即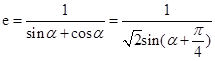 ,
,
∵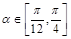 ,
,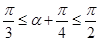
∴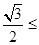
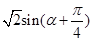 )≤1,故椭圆离心率的取值范围为
)≤1,故椭圆离心率的取值范围为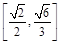 。
。
考点:本题主要考查椭圆的定义及其几何性质,两角和的正弦公式,正弦函数的图象和性质。
点评:中档题,本题利用椭圆的定义及直角三角形中的边角关系,确定得到了椭圆离心率的表达式,根据角的范围确定离心率的范围,该题综合性较强,也较为典型。

练习册系列答案
相关题目
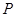 在曲线
在曲线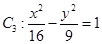 上,点Q在曲线
上,点Q在曲线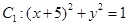 上,点R在曲线
上,点R在曲线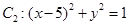 上,则
上,则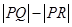 最大值是
最大值是 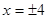 ,离心率等于
,离心率等于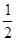 的椭圆方程是 .
的椭圆方程是 .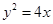 上任意一点
上任意一点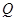 ,点
,点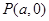 都满足
都满足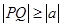 ,则
,则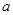 的取值范围是____ .
的取值范围是____ .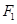 ,
,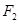 ,且它们在第一象限的交点为P,△
,且它们在第一象限的交点为P,△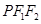 是以
是以 为底边的等腰三角形.若
为底边的等腰三角形.若 的函数称为“莫言函数”,并把其与
的函数称为“莫言函数”,并把其与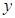 轴的交点关于原点的对称点称为“莫言点”,以“莫言点”为圆心凡是与“莫言函数”图象有公共点的圆,皆称之为“莫言圆”.当
轴的交点关于原点的对称点称为“莫言点”,以“莫言点”为圆心凡是与“莫言函数”图象有公共点的圆,皆称之为“莫言圆”.当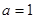 ,
,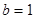 时,在所有的“莫言圆”中,面积的最小值 .
时,在所有的“莫言圆”中,面积的最小值 .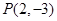 是双曲线
是双曲线 上一点,双曲线两个焦点间的距离等于4,则该双曲线方程是___________.
上一点,双曲线两个焦点间的距离等于4,则该双曲线方程是___________. 的焦点为F,准线与x轴交于M点,过M点斜率为k的直线l与抛物线C交于A、B两点,若
的焦点为F,准线与x轴交于M点,过M点斜率为k的直线l与抛物线C交于A、B两点,若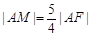 ,则
,则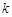 的值 .
的值 .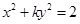 表示焦点在
表示焦点在 轴的椭圆,那么实数
轴的椭圆,那么实数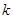 的取值范围是____________。
的取值范围是____________。