题目内容
我们把形如 的函数称为“莫言函数”,并把其与
的函数称为“莫言函数”,并把其与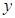 轴的交点关于原点的对称点称为“莫言点”,以“莫言点”为圆心凡是与“莫言函数”图象有公共点的圆,皆称之为“莫言圆”.当
轴的交点关于原点的对称点称为“莫言点”,以“莫言点”为圆心凡是与“莫言函数”图象有公共点的圆,皆称之为“莫言圆”.当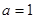 ,
,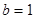 时,在所有的“莫言圆”中,面积的最小值 .
时,在所有的“莫言圆”中,面积的最小值 .
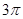
解析试题分析:当a=1,b=1时,
则函数 y=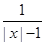 与Y轴交于(0,-1)点
与Y轴交于(0,-1)点
则“莫言点”坐标为(0,1),令“莫言圆”的标准方程为x2+(y-1)2=r2,
令“莫言圆”与函数 y=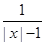 图象的左右两支相切,则切点坐标为(
图象的左右两支相切,则切点坐标为(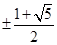 ,
,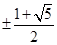 ),
),
此时r=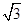 ;
;
令“莫言圆”与函数 y=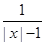 图象的下支相切,则切点坐标为(0,-1),此时r=2;
图象的下支相切,则切点坐标为(0,-1),此时r=2;
故所有的“莫言圆”中,面积的最小值为3π。
考点:本题主要考查直线与圆的位置关系,函数的图象和性质。
点评:中档题,根据“莫言圆”的圆心坐标及“莫言函数”的解析式,求出“莫言圆”的圆心到函数图象距离的最小值是解答本题的关键。

练习册系列答案
相关题目
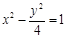 ,则此双曲线的准线方程为 .
,则此双曲线的准线方程为 .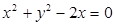 ,以原点为极点,x轴的正半轴为极轴建立极坐标系,则曲线C的极坐标方程为 __________;
,以原点为极点,x轴的正半轴为极轴建立极坐标系,则曲线C的极坐标方程为 __________;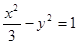 ,则此双曲线的焦点到渐近线的距离为
,则此双曲线的焦点到渐近线的距离为 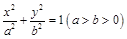 上一点
上一点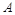 关于原点的对称点为
关于原点的对称点为 为其右焦点,若
为其右焦点,若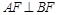 ,设
,设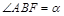 ,且
,且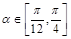 ,则该椭圆离心率的取值范围为 .
,则该椭圆离心率的取值范围为 .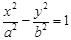 (a>0,b>0)的左、右焦点,过F1的直线与
(a>0,b>0)的左、右焦点,过F1的直线与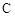 的左、右两支分别交于A,B两点.若 | AB |: | BF2 |: |AF2 |=3:4 : 5,则双曲线的离心率为 .
的左、右两支分别交于A,B两点.若 | AB |: | BF2 |: |AF2 |=3:4 : 5,则双曲线的离心率为 .  和双曲线
和双曲线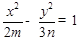 有公共的焦点,那么双曲线的渐近线方程是 .
有公共的焦点,那么双曲线的渐近线方程是 .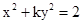 表示焦点在y轴的椭圆,那么实数k的取值范围是____________。
表示焦点在y轴的椭圆,那么实数k的取值范围是____________。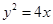 上一点
上一点 到焦点的距离为3,则点
到焦点的距离为3,则点