题目内容
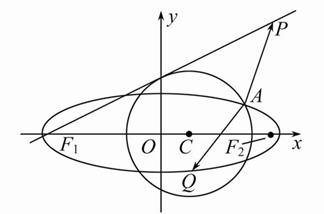
已知点P(4,4),圆C:(x-m)2+y2=5(m<3) 与椭圆E:![]() +
+![]() =1(a>b>0)有一个公共点A(3,1),F1、F2分别是椭圆的左、右焦点,直线PF1与圆C相切.
=1(a>b>0)有一个公共点A(3,1),F1、F2分别是椭圆的左、右焦点,直线PF1与圆C相切.
(1)求m的值与椭圆E的方程;
(2)设Q为椭圆E上的一个动点,求![]() ·
·![]() 的取值范围.
的取值范围.![]()
(1![]() )点A代入圆C的方程,得(3-m)2+1=5,
)点A代入圆C的方程,得(3-m)2+1=5,
∵m<3,∴m=1.圆C的方程为(x-1)2+y2=5.
设直线PF1的斜率为k,则PF1:y=k(x-4)+4,
即kx-y-4k+4=0.
∵直线PF1与圆C相切,∴![]() =
=![]() .
.
解得k=![]() ,或k=
,或k=![]() .
.
当k=![]() 时,直线PF1与x轴的交点横坐标为
时,直线PF1与x轴的交点横坐标为![]() ,不合题意,舍去.
,不合题意,舍去.
当k=![]() 时,直线PF1与x轴的交点横坐标为-4,
时,直线PF1与x轴的交点横坐标为-4,
∴c=4,F1(-4,0),F2(4,0).
2a=|AF1|+|AF2|=5![]() +
+![]() =6
=6![]() ,a=3
,a=3![]() ,
,
a2=18,b2=2.椭圆E的方程为:![]() +
+![]() =1.
=1.
(2)![]() =(1,3),设Q(x,y),
=(1,3),设Q(x,y),![]() =(x-3,y-1),
=(x-3,y-1),
![]() ·
·![]() =(x-3)+3(y-1)=x+3y-6.
=(x-3)+3(y-1)=x+3y-6.
∵![]() +
+![]() =1,即x2+(3y)2=18,
=1,即x2+(3y)2=18,
而x2+(3y)2≥2|x|·|3y|,∴-18≤6xy≤18.
则(x+3y)2=x2+(3y)2+6xy=18+6xy的取值范围是[0,36].
x+3y的取值范围是[-6,6].
∴x+3y-6的取值范围是[-12,0],
即![]() ·
·![]() 的取值范围是[-12,0].
的取值范围是[-12,0].

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知点P在曲线y=sinx上,a为曲线在点P处的切线的倾斜角,则a的取值范围是( )
A、[0,
| ||||
B、[
| ||||
C、[0,
| ||||
D、[
|
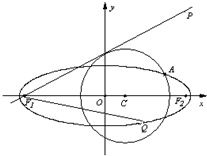 已知点P(4,4),圆C:(x-m)2+y2=5(m<3)与椭圆E:
已知点P(4,4),圆C:(x-m)2+y2=5(m<3)与椭圆E: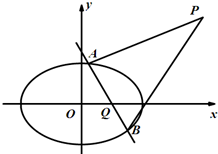 已知椭圆C:
已知椭圆C: