题目内容

已知点P在曲线y=sinx上，a为曲线在点P处的切线的倾斜角，则a的取值范围是（　　）

A、[0，

]

B、[

，

3π

]

C、[0，

]∪[

3π

，π)

D、[

3π

，π）

分析：求出导函数，根据曲线在切点处的导数值为切线的斜率，利用斜率是倾斜角的正切值，求出斜率的范围即倾斜角的正切值的范围，求出倾斜角的范围．

解答：解：y′=cosx
∴tana=cosx
∵-1≤cosx≤1
即-1≤tana≤1
∵0≤a≤π
∴0≤a≤

或

3π

≤a＜π
故选C

点评：本题考查导数的几何意义：在切点处的导数值是切线的斜率、考查倾斜角的正切值是直线的斜率、考查倾斜角的范围．

练习册系列答案

二期课改配套教辅读物系列答案

小学单元测试卷系列答案

新课程单元检测新疆电子音像出版社系列答案

冠军练加考课时作业单元期中期末检测系列答案

相关题目

，（x，y，b，c∈R），且把其中x，y所满足的关系式记为y=f（x），若f′（x）为f（x）的导函数，F（x）=f（x）+af′（x）（a＞0），且F（x）是R上的奇函数．
（Ⅰ）求

和c的值；
（Ⅱ）若函数f（x）在[

，a2]上单调递减，求b的取值范围；
（Ⅲ）当a=2时，设0＜t＜4且t≠2，曲线y=f（x）在点A（t，f（t））处的切线与曲线y=f（x）相交于点B（m，f（m））（A，B不重合），直线x=t与y=f（m）相交于点C，△ABC的面积为S，试用t表示△ABC的面积S（t），若P为S（t）上一动点，D（4，0），求直线PD的斜率的取值范围．

已知A、B分别是x轴和y轴上的两个动点，满足|AB|=2，点P在线段AB上，且

（t是不为0的常数），设点P的轨迹方程为C．
（Ⅰ）求点P的轨迹方程C；
（Ⅱ）若曲线C为焦点在x轴上的椭圆，试求实数t的取值范围；
（Ⅲ）若t=2，点M、N是C上关于原点对称的两个动点，点Q的坐标为(

，3)，求△QMN的面积S的最大值．

曲线C是中心在原点，焦点在x轴上的双曲线的右支，已知它的右准线方程为l：x=

，一条渐近线方程是y=

x，线段PQ是过曲线C右焦点F的一条弦，R是弦PQ的中点．
（1）求曲线C的方程；
（2）当点P在曲线C上运动时，求点R到y轴距离的最小值；
（3）若在直线l的左侧能作出直线m：x=a，使点R在直线m上的射影S满足

•

=0．当点P在曲线C上运动时，求a的取值范围．

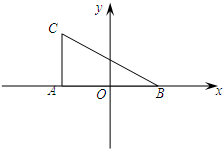如图，在Rt△ABC中，∠CAB=90°，|AB|=2，|AC|=

，点A，B关于y轴对称．一曲线E过C点，动点P在曲线E上运动，且保持|PA|+|PB|的值不变．
（1）求曲线E的方程；
（2）已知点S(0，-

)，T(0，

)，求∠SPT的最小值；
（3）若点F(1，

)是曲线E上的一点，设M，N是曲线E上不同的两点，直线FM和FN的倾斜角互补，试判断直线MN的斜率是否为定值，如果是，求出这个定值；如果不是，请说明理由．

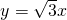曲线C是中心在原点，焦点在x轴上的双曲线的右支，已知它的右准线方程为l： $数学公式$ ，一条渐近线方程是 $数学公式$ ，线段PQ是过曲线C右焦点F的一条弦，R是弦PQ的中点．
（1）求曲线C的方程；
（2）当点P在曲线C上运动时，求点R到y轴距离的最小值；
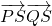（3）若在直线l的左侧能作出直线m：x=a，使点R在直线m上的射影S满足 $数学公式$ =0．当点P在曲线C上运动时，求a的取值范围．

试题分类