题目内容
已知圆C的圆心在坐标原点,且过点M(1 ,
).
(1)求圆C的方程;
(2)已知点P是圆C上的动点,试求点P到直线x+y-4=0的距离的最小值;
(3)若直线l与圆C相切,且l与x,y轴的正半轴分别相交于A,B两点,求△ABC的面积最小时直线
l的方程.
| 3 |
(1)求圆C的方程;
(2)已知点P是圆C上的动点,试求点P到直线x+y-4=0的距离的最小值;
(3)若直线l与圆C相切,且l与x,y轴的正半轴分别相交于A,B两点,求△ABC的面积最小时直线
l的方程.
分析:(1)根据圆的定义求出圆的半径,进而结合题意写出圆的方程.
(2)由圆的性质可得:P到直线l:x+y-4=0的距离的最小值是圆心到直线l的距离减去半径,结合点到直线的距离公式可得答案.
(3)设直线l的方程为:y=kx+b,根据题意可得:k<0,b>0,又因为l与圆C相切,得到b关于k的一个关系式,再用b与k表示出三角形的面积可得:S△ABC=2(-k+
)≥4,然后利用基本不等式求出面积的最大值与k、b的值即可.
(2)由圆的性质可得:P到直线l:x+y-4=0的距离的最小值是圆心到直线l的距离减去半径,结合点到直线的距离公式可得答案.
(3)设直线l的方程为:y=kx+b,根据题意可得:k<0,b>0,又因为l与圆C相切,得到b关于k的一个关系式,再用b与k表示出三角形的面积可得:S△ABC=2(-k+
| 1 |
| -k |
解答:解:(1)由题意可得:圆C的半径为|CM|=
=2,…(2分)
所以圆C的方程为x2+y2=4…(3分)
(2)圆心到直线l的距离为d=
=2
,…(4分)
所以P到直线l:x+y-4=0的距离的最小值为:2
-2…(6分)
(3)设直线l的方程为:y=kx+b,
因为l与x,y轴的正半轴分别相交于A,B两点,所以k<0,b>0,且A(-
, 0) , B(0 , b),
又因为l与圆C相切,
所以C点到直线l的距离等于圆的半径2,即:
=2⇒b2=4k2+4,①,
因为S△ABC=
(-
)b=
②…(8分)
所以将①代入②得S△ABC=
=2(-k+
)≥4
=4,
当且仅当k=-1时取等号,
所以当k=-1时,△ABC的面积最小,
此时b2=4k2+4=8, b=2
,
所以直线l的方程为:y=-x+2
…(10分)
| 1+3 |
所以圆C的方程为x2+y2=4…(3分)
(2)圆心到直线l的距离为d=
| |-4| | ||
|
| 2 |
所以P到直线l:x+y-4=0的距离的最小值为:2
| 2 |
(3)设直线l的方程为:y=kx+b,
因为l与x,y轴的正半轴分别相交于A,B两点,所以k<0,b>0,且A(-
| b |
| k |
又因为l与圆C相切,
所以C点到直线l的距离等于圆的半径2,即:
| |b| | ||
|
因为S△ABC=
| 1 |
| 2 |
| b |
| k |
| -b2 |
| 2k |
所以将①代入②得S△ABC=
| -(4k2+4) |
| 2k |
| 1 |
| -k |
(-k)•
|
当且仅当k=-1时取等号,
所以当k=-1时,△ABC的面积最小,
此时b2=4k2+4=8, b=2
| 2 |
所以直线l的方程为:y=-x+2
| 2 |
点评:解决此类问题的关键是熟练掌握圆的标准方程与圆的一个性质,以及结合点到直线的距离判断直线与圆的位置关系.

练习册系列答案
相关题目
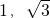 ).
). ).
).