题目内容
9.已知函数f(x)=x2+ax+3,若f(x)在区间[1,4]上为单调函数,则a的范围是a≥-2或a≤-8;变式为:已知函数f(x)=x2+ax+3.
①若y=f(x)在区间[1,4]有最大值10,则a的值为-$\frac{9}{4}$;
②若f(x)=0在区间[1,4]有两个不相等的实根,则a的范围为-4<a<-2$\sqrt{3}$;
③若f(x)=0在区间[1,4]有解,则a的范围为-$\frac{19}{4}$≤a≤-2$\sqrt{3}$;
④若y=f(x)在区间[1,4]内存在x0,使f(x0)>0,则a的范围为a>-$\frac{19}{4}$;
⑤若y=f(x)在区间[1,4]上恒为正数,则a的范围为a>-2$\sqrt{3}$.
分析 求出对称轴,讨论对称轴和区间的关系,由单调性得到a的不等式,即可得到所求范围;
对于①,考虑端点处和顶点处的函数值最大,检验即可得到;对于②,考虑f(1),f(4),判别式大于0,对称轴介于(1,4),解不等式组,即可得到所求范围;对于③,由参数分离和分式函数的最值,即可得到所求范围;对于④,可得f(1)>0或f(4)>0,解不等式即可得到;对于⑤,由参数分离和基本不等式即可得到所求范围.
解答 解:函数f(x)=x2+ax+3的对称轴为x=-$\frac{a}{2}$,
若区间[1,4]上为单调增函数,则-$\frac{a}{2}$≤1,解得a≥-2;
若区间[1,4]上为单调减函数,则-$\frac{a}{2}$≥4,解得a≤-8.
综上可得a≥-2或a≤-8;
对于①,可能为f(1)=10,或f(4)=10,或f(-$\frac{a}{2}$)=10,
即有a=6或a=-$\frac{9}{4}$或a∈∅,
当a=6时,区间[1,4]在对称轴x=-3的右边,为增区间,f(4)最大,舍去;
当a=-$\frac{9}{4}$时,区间[1,4]包含对称轴x=$\frac{9}{8}$,f(4)最大,成立.
即有a=-$\frac{9}{4}$;
对于②,由题意可得$\left\{\begin{array}{l}{f(1)=a+4>0}\\{f(4)=4a+19>0}\\{{a}^{2}-12>0}\\{1<-\frac{a}{2}<4}\end{array}\right.$,解得-4<a<-2$\sqrt{3}$;
对于③,由题意可得-a=x+$\frac{3}{x}$在[1,4]有解,由x+$\frac{3}{x}$$≥2\sqrt{3}$,又1+3<4+$\frac{3}{4}$,即有2$\sqrt{3}$≤-a≤$\frac{19}{4}$,
即有-$\frac{19}{4}$≤a≤-2$\sqrt{3}$;
对于④,由题意可得f(1)>0或f(4>0,解得a>-$\frac{19}{4}$;
对于⑤,由题意可得-a<x+$\frac{3}{x}$在[1,4]的最小值,由x+$\frac{3}{x}$$≥2\sqrt{3}$,当且仅当x=$\sqrt{3}$>1,取得最小值,
即为-a<2$\sqrt{3}$,解得a>-2$\sqrt{3}$.
故答案为:a≥-2或a≤-8,a=-$\frac{9}{4}$,-4<a<-2$\sqrt{3}$,-$\frac{19}{4}$≤a≤-2$\sqrt{3}$,a>-$\frac{19}{4}$,a>-2$\sqrt{3}$.
点评 本题考查二次函数的性质和运用,考查二次函数的值域和最值的求法,考查函数恒成立和存在问题,属于中档题和易错题.

| A. | M=A,N=B | B. | M⊆A,N=B | C. | M=A,N⊆B | D. | M⊆A,N⊆B |
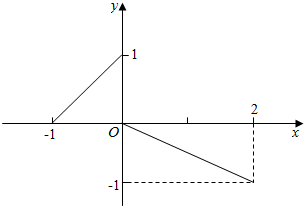
| A. | [$\frac{3}{2}$,+∞) | B. | [$\sqrt{3}$,3] | C. | [$\sqrt{3}$,+∞) | D. | [$\frac{3}{2}$,3] |