题目内容
10.已知函数f(x)=log2(x2+1),函数g(x)=($\frac{1}{3}$)x-m.若?x1∈[0,3],?x2∈[1,2],使得f(x1)≥g(x2),则m的取值范围是( )| A. | [$\frac{1}{9}$,+∞) | B. | [$\frac{1}{3}$,+∞) | C. | (-∞,$\frac{1}{9}$] | D. | (-∞,$\frac{1}{3}$] |
分析 要使命题成立需满足f(x1)min≥g(x2)min,利用函数的单调性,可求最值,即可得到实数m的取值范围.
解答 解:∵当x1∈[0,3]时,函数f(x)是增函数,
∴f(x1)∈[0,log210];
∵g(x)=($\frac{1}{3}$)x-m在[1,2]上是减函数,
∴当x2∈[1,2]时,g(x2)∈[$\frac{1}{9}$-m,$\frac{1}{3}$-m].
要使命题成立需满足f(x1)min≥g(x2)min,
即0≥$\frac{1}{9}$-m,
解得m≥$\frac{1}{9}$,
故选:A
点评 本题考查函数恒成立问题,解决的常用方法是转化为函数的最值问题进行处理.,考查学生逻辑思维,分析解决问题的能力.要使命题成立需满足f(x1)min≥g(x2)min,是解题的关键,属于中档题.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
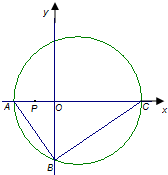 如图,直角三角形ABC的顶点坐标A(-2,0),直角顶点$B(0,-2\sqrt{2})$,顶点C在x轴上,点P为线段OA的中点.
如图,直角三角形ABC的顶点坐标A(-2,0),直角顶点$B(0,-2\sqrt{2})$,顶点C在x轴上,点P为线段OA的中点.