题目内容
(本小题满分10分)
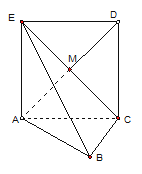
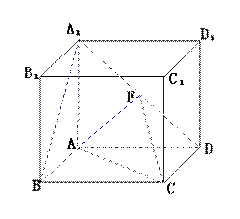
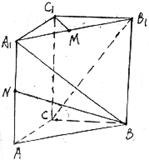
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,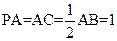 ,N为AB上一点,AB="4AN," M、S分别为PB,BC的中点.以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立如图空间直角坐标系.
,N为AB上一点,AB="4AN," M、S分别为PB,BC的中点.以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立如图空间直角坐标系.
(Ⅰ)证明:CM⊥SN;
(Ⅱ)求SN与平面CMN所成角的大小.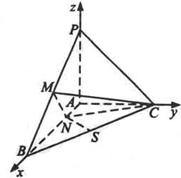
(Ⅰ) ,因为
,因为 ,
,
所以CM⊥SN
(Ⅱ)SN与平面CMN所成角为45°
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若直线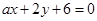 和直线
和直线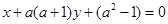 垂直,则
垂直,则 的值为( )
的值为( )
A. 或 或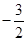 | B. 或 或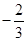 | C. 或 或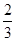 | D. 或 或 |
如图,直线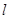 经过二、三、四象限,
经过二、三、四象限,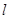 的倾斜角为
的倾斜角为 ,斜率为k,则 ( ).
,斜率为k,则 ( ).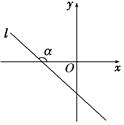
A.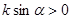 | B.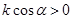 | C.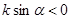 | D.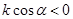 |
曲线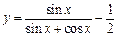 在点
在点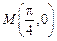 处的切线与直线
处的切线与直线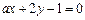 互相垂直,则a为( )
互相垂直,则a为( )
| A.4 | B.2 | C.1 | D.3 |

 BCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=
BCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB= ,BC=1,PA=2,E为PD的中点.
,BC=1,PA=2,E为PD的中点.
 的棱长为
的棱长为 ,点
,点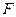 为
为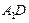 的中点.
的中点.

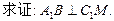
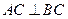
 ,且AC=BC.
,且AC=BC.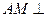 平面EBC;w.w.zxxk.c.o
平面EBC;w.w.zxxk.c.o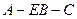 的大小.
的大小.