题目内容
(12分)
如图,边长为2的正方形ACDE所在的平面与平面ABC垂直,AD与CE的交点为M,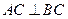
 ,且AC=BC.
,且AC=BC.
(1)求证: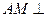 平面EBC;w.w.zxxk.c.o
平面EBC;w.w.zxxk.c.o
(2求二面角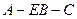 的大小.
的大小.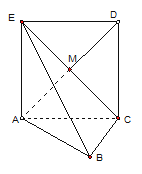
略
解析解: ∵四边形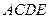 是正方形 ,w.w.w.zxxk.c.o.m
是正方形 ,w.w.w.zxxk.c.o.m 

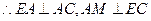 ,
,
∵ 平面
平面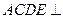 平面
平面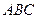 ,
,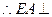 平面
平面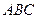 ,
,
∴可以以点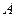 为原点,以过
为原点,以过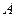 点平行于
点平行于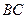 的直线为
的直线为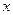 轴,
轴,
分别以直线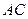 和
和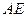 为
为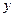 轴和
轴和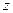 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系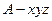 .
.
设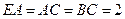 ,则
,则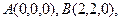
 ,
,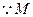 是正方形
是正方形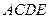 的对角线的交点
的对角线的交点 ,
,
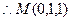 .
.
(1)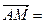
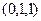 ,
, ,
,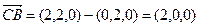 ,
, ,
, 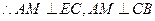 w.w.w.zxxk.c.o.m
w.w.w.zxxk.c.o.m 

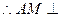 平面
平面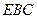 .
.
(2) 设平面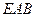 的法向量为
的法向量为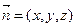 ,则
,则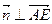 且
且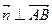 ,
,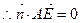 且
且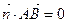 .
.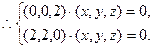 即
即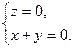 w.w.w.zxxk.c.o.m
w.w.w.zxxk.c.o.m 


取 ,则
,则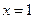 , 则
, 则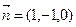 .
.
又∵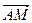 为平面
为平面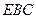 的一个法向量,且
的一个法向量,且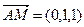 ,
, ,
,
设二面角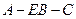 的平面角为
的平面角为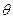 ,则
,则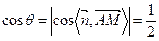 ,
,
∴二面角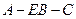 等于
等于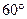 .
.
(1) ,(2)均可用几何法

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
、过点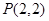 的直线与圆
的直线与圆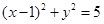 相切,且与直线
相切,且与直线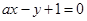 垂直,则
垂直,则 ( ).
( ).
A.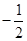 | B.1 | C.2 | D. |
已知两直线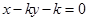 与
与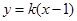 平行,则
平行,则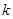 的值为( )
的值为( )
A.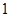 | B.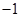 | C.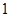 或 或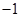 | D.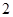 |
经过点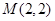 且在两轴上截距相等的直线是( )
且在两轴上截距相等的直线是( )
A.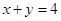 | B.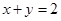 |
C.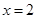 或 或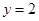 | D.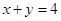 或 或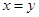 |
已知圆 ,圆
,圆 ,
,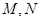 分别是圆
分别是圆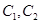 上的动点,
上的动点,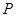 为
为 轴上的动点,则
轴上的动点,则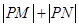 的最小值为 ( )
的最小值为 ( )
A.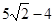 | B.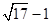 | C.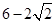 | D.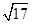 |
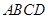 -
-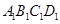 中,
中,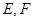 分别为
分别为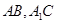 的中点. 应用空间向量方法求解下列问题.
的中点. 应用空间向量方法求解下列问题. 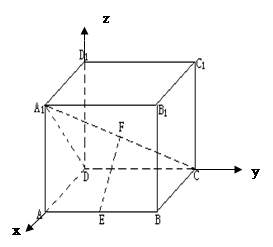
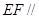 平面
平面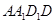 ;
;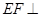 平面
平面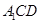 .
.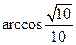 ,求BD的长度.(15分)
,求BD的长度.(15分)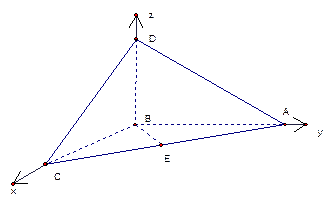
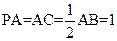 ,N为AB上一点,AB="4AN," M、S分别为PB,BC的中点.以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立如图空间直角坐标系.
,N为AB上一点,AB="4AN," M、S分别为PB,BC的中点.以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立如图空间直角坐标系.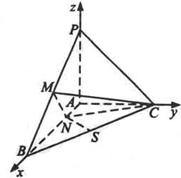
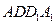 和三棱锥
和三棱锥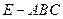 组合而成,点
组合而成,点 、
、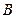 、
、 在圆
在圆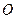 的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图3所示,其中
的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图3所示,其中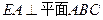 ,
,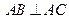 ,
,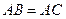 ,
,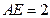 .
.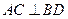 ;
;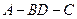 的平面角的大小.
的平面角的大小.