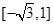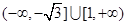题目内容
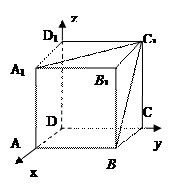
如图,直三棱柱ABC—A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1,A1A的中点;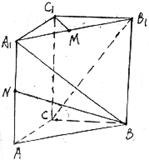
(1)求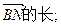
(2)求
(3)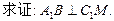
(4)求CB1与平面A1ABB1所成的角的余弦值.
如图,建立空间直角坐标系O—xyz.(1)依题 意得B(0,1,0)、N(1,0,1)
意得B(0,1,0)、N(1,0,1)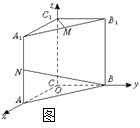
∴|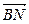 |=
|=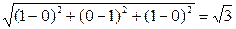 .
.
(2)依题意得A1(1,0,2)、B(0,1,0)、C(0,0,0)、B1(0,1,2)
∴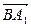 ={-1,-1,2},
={-1,-1,2},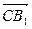 ={0,1,2,},
={0,1,2,},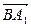 ·
·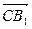 =3,|
=3,|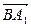 |=
|=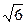 ,|
,|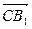 |=
|=
∴cos<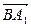 ,
,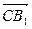 >=
>=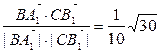 .
.
(3)证明:依题意,得C1(0,0,2)、M(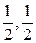 ,2),
,2), ={-1,1,2},
={-1,1,2},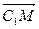 ={
={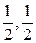 ,0}.∴
,0}.∴ ·
·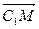 =-
=-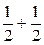 +0=0,∴
+0=0,∴ ⊥
⊥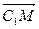 ,∴A1B⊥C1M.
,∴A1B⊥C1M.
解析

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
直线x+y﹣1=0的倾斜角为( ).
A.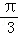 | B.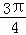 | C.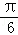 | D.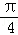 |
与直线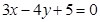 关于x轴对称的直线方程为( )
关于x轴对称的直线方程为( )
A. | B.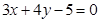 |
C. | D. |
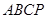 中,
中,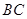 ∥
∥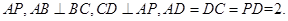
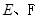 分别是
分别是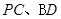 的中点,现将
的中点,现将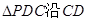 折起,使
折起,使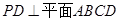 ,
,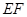 ∥平面
∥平面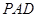 ;
;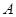 到平面
到平面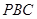 的距离.
的距离.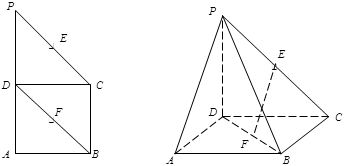
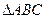 的三个顶点坐标为分别为:
的三个顶点坐标为分别为: 试判断
试判断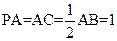 ,N为AB上一点,AB="4AN," M、S分别为PB,BC的中点.以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立如图空间直角坐标系.
,N为AB上一点,AB="4AN," M、S分别为PB,BC的中点.以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立如图空间直角坐标系.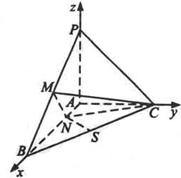
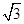 )直线
)直线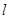 过原点,且与线段AB有交点,则直线
过原点,且与线段AB有交点,则直线