题目内容
已知数列{an}的前n项和为Sn,3Sn=an-1(n∈N?).
(1)求a1,a2;
(2)求证:数列{an}是等比数列;
(3)求an和Sn.
(1)求a1,a2;
(2)求证:数列{an}是等比数列;
(3)求an和Sn.
(1)a1=-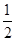 . a2=
. a2= (2)见解析(3)
(2)见解析(3)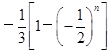
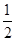 . a2=
. a2= (2)见解析(3)
(2)见解析(3)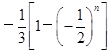
(1)解:由3S1=a1-1,得3a1=a1-1,∴a1=-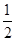 .
.
又3S2=a2-1,即3a1+3a2=a2-1,得a2= .
.
(2)证明:当n≥2时,an=Sn-Sn-1= (an-1)-
(an-1)- (an-1-1),得
(an-1-1),得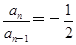 ,所以{an}是首项为-
,所以{an}是首项为-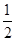 ,公比为-
,公比为-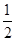 的等比数列.
的等比数列.
(3)解:由(2)可得an=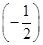 n,Sn=
n,Sn=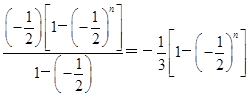 .
.
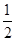 .
.又3S2=a2-1,即3a1+3a2=a2-1,得a2=
 .
.(2)证明:当n≥2时,an=Sn-Sn-1=
 (an-1)-
(an-1)- (an-1-1),得
(an-1-1),得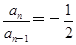 ,所以{an}是首项为-
,所以{an}是首项为-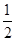 ,公比为-
,公比为-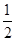 的等比数列.
的等比数列.(3)解:由(2)可得an=
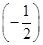 n,Sn=
n,Sn=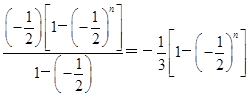 .
.
练习册系列答案
相关题目
 排成一列,称为向量列,记作
排成一列,称为向量列,记作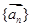 ,又设
,又设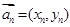 ,假设向量列
,假设向量列 ,
, 。
。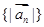 是等比数列;
是等比数列;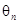 表示向量
表示向量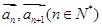 间的夹角,若
间的夹角,若 ,记
,记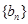 的前
的前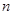 项和为
项和为 ,求
,求 ;
; 是
是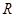 上不恒为零的函数,且对任意的
上不恒为零的函数,且对任意的 ,都有
,都有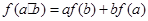 ,若
,若 ,
, ,求数列
,求数列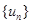 的前
的前 .
.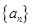 中,
中, ,对任意
,对任意 ,函数
,函数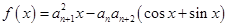 满足
满足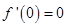 ,
,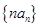 的前
的前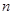 项和
项和 。
。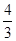 ,则{an}的前10项和为________.
,则{an}的前10项和为________.