题目内容
已知向量a=3e1-2e2,b=4e1+e2,其中e1=(1,0),e2=(0,1),求:
(1)a·b,|a+b|;(2)a与b的夹角的余弦值.
(1)10,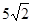 ;(2)
;(2)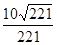 .
.
解析试题分析:先根据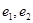 向量是互相垂直的单位向量表示出向量要用的两个向量,然后根据向量的数量积运算和向量模的运算求出答案.(2)先求出向量的模长,然后根据cosθ的表示式将数值代入即可得到答案.本题主要考查向量的模、平面向量的坐标运算、数量积运算,本题解题的关键是根据所给的两个单位向量,写出要用的向量的坐标.
向量是互相垂直的单位向量表示出向量要用的两个向量,然后根据向量的数量积运算和向量模的运算求出答案.(2)先求出向量的模长,然后根据cosθ的表示式将数值代入即可得到答案.本题主要考查向量的模、平面向量的坐标运算、数量积运算,本题解题的关键是根据所给的两个单位向量,写出要用的向量的坐标.
(1)a=3(1,0)-2(0,1)=(3,-2),b=4(1,0)+(0,1)=(4,1),a·b=3×4+(-2)×1=10,
∵|a+b|2=(a+b)2=a2+2a·b+b2=|a|2+20+|b|2=13+20+17=50,∴|a+b|=5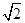
(2)cos〈a,b〉=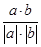 =
=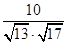 =
=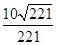 .
.
考点:平面向量数量积的坐标表示、模、夹角.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
 满足|
满足| |=|
|=| |=1,且|2
|=1,且|2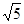 .
. 的值;
的值;  与
与 夹角
夹角 .
.
 ,求x的范围;
,求x的范围; 的最大值以及此时x的值.
的最大值以及此时x的值. :
: 的焦点为
的焦点为 ,若过点
,若过点 的直线与抛物线相交于
的直线与抛物线相交于 两点,且
两点,且 .
. 为抛物线
为抛物线 ,
, 为
为 的最小值.
的最小值.
 ,
,
 ,
,  的值。
的值。 为何值时,
为何值时,
 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向? ,
, ,(1)若
,(1)若 与
与 垂直,求
垂直,求 的值;(2)若
的值;(2)若 ,求
,求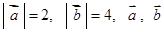 的夹角为
的夹角为 .
. 的值;
的值; 的大小.
的大小.
 ;
; ,求k的值.
,求k的值. 且
且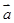 在
在 方向上的投影等于
方向上的投影等于 =____________。
=____________。